Перед тим, як вирішувати поставлену задачу, потрібно переконатися, що дисперсії порівнюваних сукупностей однакові (див. п. 4.1). Далі рішення здійснюється в такий спосіб: висувається основна й альтернативна гіпотези. Розглянемо три випадки:
а) Н0: M(Х) = M(У) б) Н0:M(Х) = M(У) в) Н0: M(Х) = M(У)
Н1: M(Х) > M(У) Н1: M(Х) < M(У) Н1: M(Х) ¹ M(У)
Для перевірки гіпотез за результатами вибірок обчислюємо спостережуване значення критерію
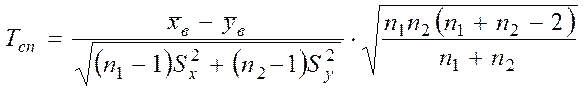 .
.
Цей критерій є випадковою величиною, що підкоряється закону розподілу Стьюдента з k = n1 + n2 – 2 степенями вільності.
Критичні області і точки залежать від висунутих альтернативних гіпотез H1;
а) Н1: M(Х) > M(У)
Критична область є правобічною. Критична точка знаходиться за таблицею критичних точок розподілу Стьюдента (Додаток Ж, однобічна критична область): tкр = t(a ; k),
де a – заданий рівень значущості.
Якщо в результаті порівняння виявиться ôTспô
< tкр, то немає підстав відкинути нульову гіпотезу H0;
якщо ж ô Tсп ô > tкр , те нульова
гіпотеза H0 відкидається; приймається гіпотеза H1;
б) Н1: M(Х) < M(У)
Критична область є лівосторонньою. Критична точка знаходиться за таблицею критичних точок розподілу Стьюдента (Додаток Ж, однобічна критична область), тільки з від’ємним знаком: tкр = – t(a; k),
де a – заданий рівень значущості.
Якщо в результаті порівняння виявиться Tсп > tкр, то немає підстав відкинути нульову гіпотезу H0; якщо ж Tсп < tкр , то нульова гіпотеза H0 відкидається; приймається гіпотеза H1;
в) Н1: M(Х) ¹ M(У)
Критична область є двосторонньою. Критична точка знаходиться за таблицею критичних точок розподілу Стьюдента (Додаток Ж, двостороння критична область): tкр = t(a; k),
де a – заданий рівень значущості.
Якщо в результаті порівняння виявиться ô Tсп ô< tкр, то немає підстав відкинути нульову гіпотезу H0; якщо ж ô Tсп ô> tкр, то нульовагіпотеза H0 відкидається; приймається гіпотеза H1.
Нехай у двох генеральних сукупностях (С1 і С2) виконуються незалежні випробування. В результаті кожного випробування подія А може з'явитися в першій сукупності з невідомою ймовірністю р1, у другий – з невідомою ймовірністю р2.
Маємо параметри вибірок
по С1: n1 – кількість випробувань;
m1 – частота появи події А в цих випробуваннях,
w1 = m1/ n1– відносна частота (вибіркова частка) події А в сукупності С1.
по С2: n2 – кількість випробувань;
m2 – частота появи події А в цих випробуваннях,
w2 = m2/ n2– відносна частота (вибіркова частка) події А в сукупності С2.
Потрібно при заданому рівні значущості a установити рівність імовірностей р1 і р2 .
Висунемо основну й альтернативну гіпотези. Розглянемо три випадки:
а) Н0: р1 = р2 б) Н0: р1 = р2 в) Н0: р1 = р2
Н1: р1 > р2 Н1: р1 < р2 Н1: р1 ¹ р2
Для перевірки гіпотез за результатами вибірок обчислюємо спостережуване значення критерію
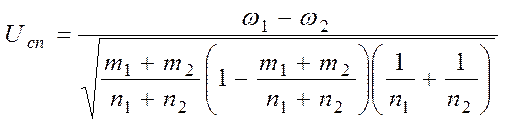 .
.
Критичні області і точки залежать від висунутих альтернативних гіпотез H1;
б) Н1: р1 > р2
Критична область є правобічної. Критична точка uкр знаходиться з рівності Ф(uкр)= (1–2a)/2 , де функція Лапласа Ф(х) задається таблицею (Додаток Б); a – заданий рівень значущості.
Якщо в результаті порівняння виявиться Uсп < uкр, то немає підстав відкинути нульову гіпотезу H0; якщо ж Uсп > uкр, то нульова гіпотеза H0 відкидається; приймається гіпотеза H1;
в) Н1: р1 < р2
Критична область є лівосторонньої. Спочатку знаходять допоміжну точку uкр' з рівності Ф(uкр')= (1–2a)/2, тоді критична точка дорівнює uкр = – uкр' .
Якщо в результаті порівняння виявиться Uсп > uкр, то немає підстав відкинути нульову гіпотезу H0; якщо ж Uсп < uкр, то нульова гіпотеза H0 відкидається; приймається гіпотеза H1.
д) Н1: р1 ¹ р2
Критична область є двосторонньої. Критична точка uкр знаходиться з рівності Ф(uкр)= (1–a)/2 , де функція Лапласа Ф(х) задається таблицею (Додаток Б).
Якщо в результаті порівняння виявиться ½Uсп½ < uкр, то немає підстав відкинути нульову гіпотезу H0; якщо ж ½Uсп½ > uкр, то нульова гіпотеза H0 відкидається; приймається гіпотеза H1.
Нехай емпіричний розподіл задається інтервальним статистичним рядом
|
Інтервал |
х 1 – х 2 |
х 2 – х 3 |
… |
х i – х i+1 |
… |
х m – х m+1 |
|
ni |
n 1 |
n 2 |
… |
n i |
… |
n m |
Обсяг вибірки дорівнює n = n 1+ n 2+…+nm .
Потрібно при заданому рівні значущості a перевірити, чи підкоряється генеральна сукупність обраному теоретичному закону розподілу f(x).
Висунемо гіпотези:
Н0: Ознака Х підкоряється закону розподілу f(x)
Н1: Ознака Х не підкоряється закону розподілу f(x)
Для перевірки сформульованих гіпотез за допомогою критерію Пірсона необхідно виконати ряд розрахунків.
а) визначають по вибірці параметри обраного теоретичного розподілу f(x). Нехай r - число параметрів розподілу.
б) для кожного інтервалу Х обчислюють імовірності потрапляння ознаки Х в даний інтервал. Для цього використовують формулу з теорії ймовірності
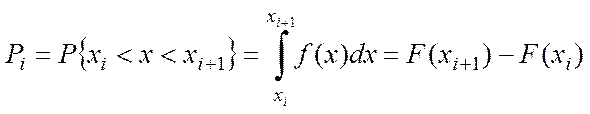 .
.
Тут f(x) – диференціальна функція розподілу, F(x) – інтегральна функція розподілу. Для багатьох видів розподілу є таблиці значень f(x) і F(x);
в) визначають теоретичні частоти
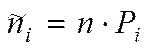 .
.
Оскільки за критерієм Пірсона вимагається, щоб теоретична частота в кожнім інтервалі була не менше п'яти, то в противному випадку допускається об'єднання стоячих поряд інтервалів з малими частотами;
д) обчислюють спостережуване значення критерію (його ще називають критерієм згоди Пірсона):
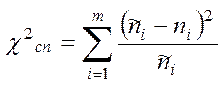 .
.
Цей критерій є випадковою величиною, що підкоряється закону розподілу χ2 (Хі – квадрат). Число степенів вільності дорівнює k = m – r – 1,
де m – число інтервалів статистичного ряду після об'єднання,
r - число параметрів обраного розподілу;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.