åni(ui+1)2 = 117; åniui2 = 141; åniui = –37, n = 50
Підставляємо: 117 = 141 + 2·(–37) + 50 . Вірно.
З таблиці знаходимо умовні моменти:
М1 = -37/50 = –0,74; М2 = 141/50 = 2,82.
Вибіркова середня дорівнює:
=М1·h
+C = –0,74×1,48+8,38= 7,2848.
Вибіркова дисперсія дорівнює:
Dв = [M2 - (M1)2]·h2 = [2,82 – (-0,742]·1,482 = 4,97746.
2,23102.
S 2 =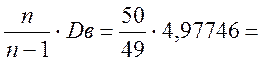 
5,07905;
2,25367.
Позначимо результат S у = 2,254.
Отримані результати дозволяють зробити наступні висновки.
Середня продуктивність праці робочого очисного вибою для стругових установок на антрацитових шахтах по вибірці дорівнює 7,28 т за вихід. Середній розкид продуктивності праці робочого очисного вибою для стругових установок на антрацитових шахтах навколо середнього по вибірці дорівнює 2,25 т за вихід.
3 Інтервальні оцінки параметрів розподілу
Інтервальною називають оцінку, що задається інтервалом, який покриває оцінюваний параметр генеральної сукупності. Довірчим називається інтервал (a,b), що із заданою імовірністю g покриває оцінюваний параметр генеральної сукупності. Імовірність g попадання оцінюваного параметра в довірчий інтервал (a,b) називається довірчою імовірністю (надійністю).
Довірчий інтервал для оцінки математичного сподівання a нормально розподіленої кількісної ознаки Х при відомому середньому квадратичному відхиленні s генеральної сукупності задається формулою:
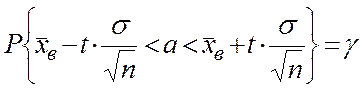, (3.1)
де g = 2Ф(t) – довірча ймовірність; Ф(t ) знаходять за таблицею Додатка 2;
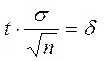– точність
оцінки.
Дана формула застосовується для оцінки математичного сподівання М(Х) = а в двох випадках:
1) якщо відомо СКВ s(х)=s;
2) якщо СКВ невідомо, але обсяг
вибірки досить великий
(n > 30). У цьому випадку в якості s беруть її оцінку S.
Довірчий інтервал для оцінки математичного сподівання a нормально розподіленої кількісної ознаки Х при відомому середньому квадратичному відхиленні s генеральної сукупності задається формулою:
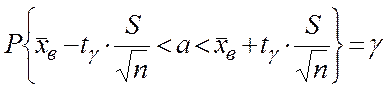, (3.2)
де tg = t(g,n) - знаходять за таблицею Додатка 3;
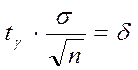– точність оцінки.
Довірчий інтервал для оцінки середнього квадратичного відхилення s нормально розподіленої кількісної ознаки Х задається формулою:
P{S(1 – q) < s <S(1+q)} = g , при q < 1 (3.3)
P{0 < s <S(1+q)} = g , при q > 1 . (3.4)
Тут виправлене вибіркове середнє квадратичне відхилення S служить оцінкою для генерального середнього квадратичного відхилення s;
q =q(g,n) – знаходять за таблицею Додатка 4;
n – обсяг вибірки; g – довірча імовірність;
d = q×S – точність оцінки.
Довірчий інтервал для оцінки невідомої імовірності p біноміального розподілу по відносній частоті w (вибірковій частці) має вид
P{p1 < p < p2} = g, (3.5)
де р = Р(А) – невідома імовірність події А;
а кінці інтервалу p1 і p2 визначаються в такий спосіб:
а) загальний випадок:
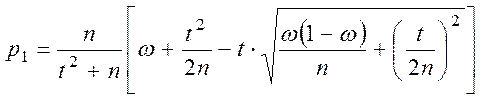
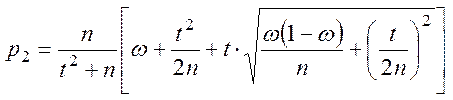, (3.6)
де n – обсяг вибірки;
g – довірча імовірність;
t – знаходиться з умови 2Ф(t) = g; Ф(t ) знаходять за таблицею Додатка 2;
вибіркова частка w знаходиться за формулою w= m/n, де n – загальне число іспитів; m – число іспитів, у яких з'явилася подія А.
b) Окремий випадок – n велике (порядку сотень):
, 
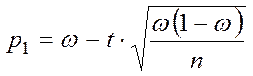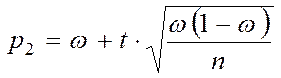(3.7)
с) Окремий випадок – відомий обсяг генеральної сукупності N і n – велике:
,
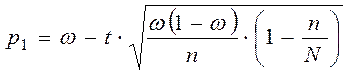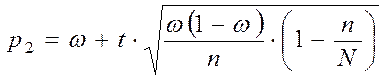. (3.8)
Приведемо приклади розрахунку довірчих інтервалів.
Приклад1.
Побудуємо 95% довірчі інтервали для оцінки математичного сподівання і СКВ генеральної сукупності ознаки Х із задачі 1, завдання 4.
Для ознаки Х маємо:
= 1,14 м; S = 0,16 м; n =50
Для оцінки математичного сподівання використовуємо формулу (3.2)
при g =0,95. За таблицею Додатка 3 знаходимо tg = t(0,95;50)=2,009. Підставляючи у формулу (3.2), одержимо
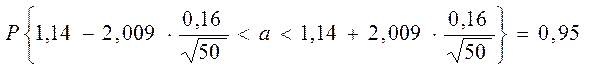
Остаточно, 
.
Отже, середня потужність
пласта по всій генеральній сукупності знаходиться в межах від 1,09 м до 1,19 м.
Надійність цього прогнозу дорівнює 95%.
Для оцінки СКВ по таблиці Додатка 4 знаходимо
q= q(0,95;50)=0,21. Підставляючи у формулу (3), одержимо
P{0,16(1 – 0,21) < s <0,16(1+0,21)} = 0,95.
Остаточно, P{0,13 < s <0,19} = 0,95. Отже, середній розкид потужності пласта навколо середньої по всій генеральній сукупності знаходиться в межах від 0,13 м до 0,19 м. Надійність цього прогнозу дорівнює 95%.
Побудова довірчих інтервалів для ознаки У проводиться аналогічно.
Приклад 2. Об'єднання закуповує партію перфораторів у кількості 1000 шт. За попередньою домовленістю об'єднання бере товар за ціною S, якщо частка нестандартної продукції у всій партії не перевищує 3%; якщо ж ця частка знаходиться в межах від 3% до 8%, то виробник дає знижку на 10%, якщо частка в межах від 8% до 20%, то передбачається знижка на 25%. При долі нестандартного товару більше чим на 20%, об'єднання відмовляється від запропонованої угоди. Для перевірки якості товару була зроблена вибірка обсягом 60 шт. З них не пройшли контроль 6 перфораторів. Чи слід об'єднанню купувати запропоновану партію, і за якою ціною? При розрахунках пропонується взяти надійність прогнозу 90%.
Нехай подія А – перфоратор виявився нестандартним.
Тоді р = Р(А) є невідомою ймовірністю, яку потрібно оцінити по вибірці за результатами іспитів і зробити висновок про можливість та умови угоди.
Запишемо вихідні дані задачі:
N = 1000; n = 60; m = 6; g = 0,9.
Вибіркова частка дорівнює w = 6/60 = 0,1.
Для побудови довірчого інтервалу використовуємо формули (3.5), (3.8).
Маємо : 2Ф(t) = 0,9. Звідси Ф(t) = 0,45. За таблицею Додатка 2 маємо t=1,64. Підставляємо у формулу (5) і знаходимо верхню і нижню границі шуканої ймовірності:
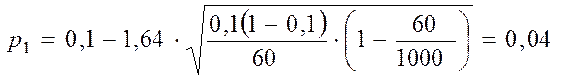
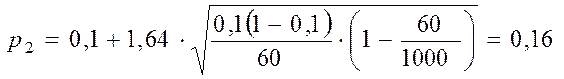
Отже, з надійністю прогнозу 90% можна стверджувати, що відсоток нестандартної продукції у всій закуповуваній партії перфораторів знаходиться в межах від 4% до 16%. Виходить, партію перфораторів можна купити, але при цьому вимагати скидку у виробника на 25%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.