Якщо врахувати формули середніх і дисперсії ознак Х и У, то розрахунок можна вести за наступними формулами:
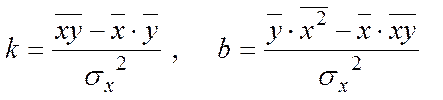 , (5.5)
, (5.5)
де
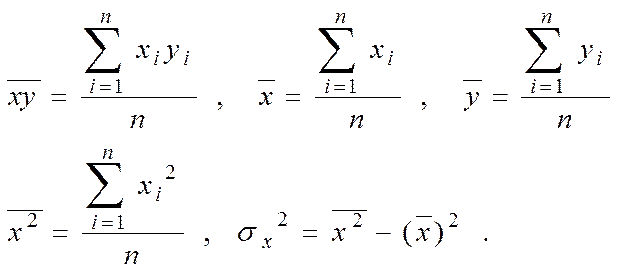 (5.6)
(5.6)
Зауваження 1. Для перевірки правильності
розрахунків можна використовувати тотожність: ![]()
Зауваження 2. У формулах (5.5) можна використовувати вибіркові
середні і дисперсії, знайдені раніше на етапі одномірного аналізу ознак
(п.2.2.4), тільки треба обчислити середній добуток 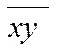 за
групованими даними (х, у) по кореляційній решітці.
за
групованими даними (х, у) по кореляційній решітці.
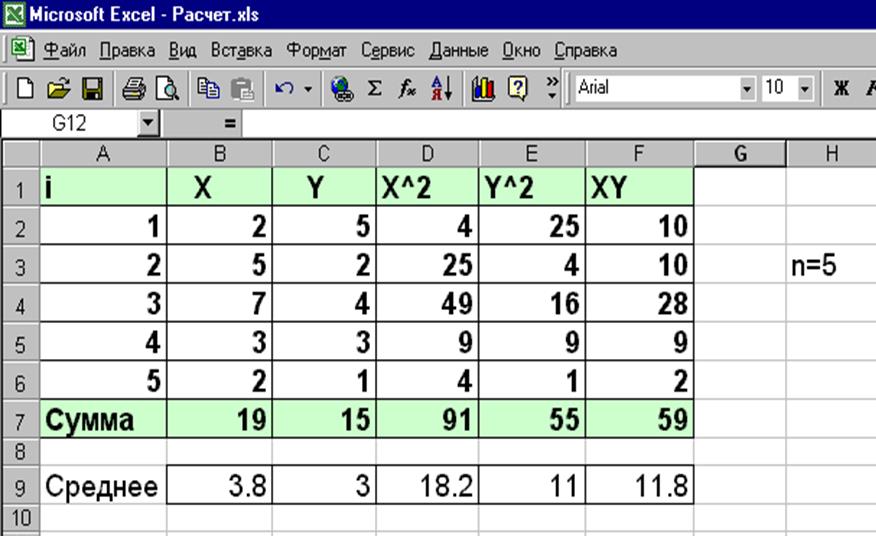
Розрахунок сум, представлених у формулах, зручно робити за допомогою табличного процесора Excel, що є електронною версією таблиць. Для розрахунку в Excel необхідно організувати розрахункову таблицю. Її вид у комп'ютері буде такий (для приклада узята вибірка обсягом n = 5):

б) Вибіркове лінійне рівняння регресії
Вибіркове лінійне рівняння регресії У на Х має вид:
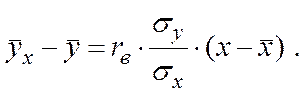 (5.7)
(5.7)
Вибіркове лінійне рівняння регресії Х на У має вид:
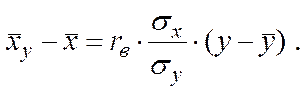 (5.8)
(5.8)
У цих рівняннях використовуються наступні оцінки (див. формули (5.6)):
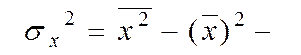 дисперсія ознаки Х;
дисперсія ознаки Х;
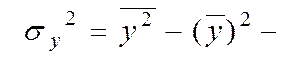 дисперсія ознаки У;
дисперсія ознаки У;
де ![]() – вибіркова середня ознаки Х;
– вибіркова середня ознаки Х;
![]() – вибіркова середня ознаки У;
– вибіркова середня ознаки У;
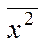 – вибірковий середній квадрат ознаки
Х;
– вибірковий середній квадрат ознаки
Х;
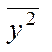 – вибірковий середній квадрат ознаки
У;
– вибірковий середній квадрат ознаки
У;
![]() – вибірковий середній додаток ознак Х
і У;
– вибірковий середній додаток ознак Х
і У;
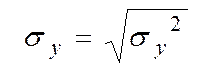 – вибіркове СКВ ознаки У;
– вибіркове СКВ ознаки У;
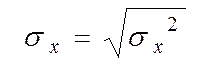 – вибіркове СКВ ознаки У;
– вибіркове СКВ ознаки У;
rв – вибірковий коефіцієнт кореляції, що обчислюється за формулою:
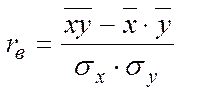 . (5.9)
. (5.9)
Якщо параметри рівняння були розраховані по рівнянню регресії з кутовим коефіцієнтом, то вибірковий коефіцієнт кореляції обчислюється за формулою:
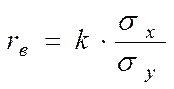 .
(5.10)
.
(5.10)
Вибірковий коефіцієнт кореляції rв є відносний показник, що характеризує силу зв’язку між признаками. При будь-яких розрахунках він знаходиться в межах від –1 до +1.
Нехай ознаки Х и У розподілені нормально. З генеральної сукупності взята вибірка обсягу n і по ній знайдено вибірковий коефіцієнт кореляції rв . Треба перевірити гіпотезу про значущість генерального коефіцієнта кореляції rг .
Висуваються гіпотези:
Основна гіпотеза Н0 : rг = 0
Конкуруюча гіпотеза Н1 : rг ≠ 0
Для перевірки гіпотези H 0 обчислюється спостережуване значення критерію:
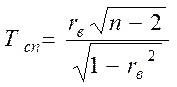 .
.
Цей критерій є випадковою величиною, що підкоряється закону розподілу Стьюдента з k = n – 2 степенями вільності. Критична область є двосторонньою. За таблицею критичних точок розподілу Стьюдента (Додаток Ж) визначається критичне значення критерію при обраному рівні значущості помилки a і числі степенів вільності k :
tкр = tкр (α; k).
Якщо Тсп > tкр , то нульова гіпотеза відкидається. Це означає, що коефіцієнт кореляції значимо відрізняється від нуля, і ознаки Х та У корельовані. У цьому випадку можна казати, що ознаки Х та У зв’язані лінейною залежністю.
Якщо Тсп < tкр , то нульова гіпотеза не відкидається. Це означає, що коефіцієнт кореляції незначимо відрізняється від нуля, і ознаки Х та У некорельовані. Прийняття гіпотези Н0 : rг = 0 зовсім не означає, що ознаки Х та У незалежні один від одного. Якщо rг = 0, то звідси випливає тільки те, що ознаки Х та У не зв’язані лінійною залежністю. Отож, вони можуть пов’язані якимсь нелінійним зв’язком.
Теоретичний коефіцієнт детермінації і теоретичне кореляційне відношення визначаються по рівнянню регресії :
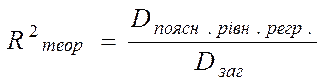 ,
(5.11)
,
(5.11)
де Dпоясн.рівн.регрес. – дисперсія результативної ознаки У, пояснена рівнянням регресії;
Dзаг – загальна дисперсія результативної ознаки У, які обчислюються за формулами:
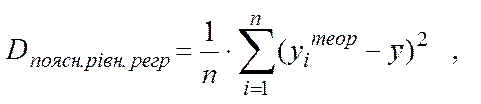
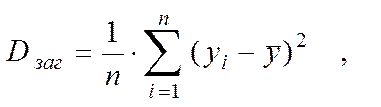 (5.12)
(5.12)
де n – обсяг вибірки;
yi – індивідуальні значення результативної ознаки У ;
![]() – середнє
значення ознаки У;
– середнє
значення ознаки У;
yiтеор – індивідуальні значення результативної ознаки У, розраховані по рівнянню регресії: yiтеор=f(xi).
Якщо рівняння регресії лінійне, то yiтеор=kxi + b, а кореляційне відношення збігається з модулем коефіцієнта кореляції η = êrв ê, коефіцієнт детермінації дорівнює R2= rв2 .
Коефіцієнт детермінації характеризує тісноту зв'язку між ознаками. У кількісній формі він указує, яка частина загальної дисперсії результативної ознаки У пояснюється варіаціями ознаки Х. Наприклад, якщо побудована статистична модель, що описує залежність обсягу добового видобутку вугілля (У) від потужності пласта (Х) і коефіцієнт детермінації дорівнює R2 = 0,56, то це значить, що по обраній моделі 56% дисперсії обсягу добового видобутку вугілля пояснюється варіацією потужності пласта.
Для одержання висновків про практичну значимість синтезованих моделей використовуються якісні оцінки, що даються на основі шкали Чедока [8].
|
R2 |
0,1 – 0,3 |
0,3 – 0,5 |
0,5 – 0,7 |
0,7 – 0,9 |
0,9 – 0,99 |
|
Характеристика сили зв'язку |
слабка |
помірна |
помітна |
висока |
дуже висока |
Якщо графік регресії – крива
лінія, то кореляцію називають криволінійною. Параметри рівняння криволінійної
регресії ![]() знаходять за методом найменших
квадратів, а в деяких випадках зводять задачу до лінійної регресії шляхом
впровадження відповідних замін. Нижче приводяться найбільш типові випадки
криволінійної регресії й формули розрахунків її параметрів:
знаходять за методом найменших
квадратів, а в деяких випадках зводять задачу до лінійної регресії шляхом
впровадження відповідних замін. Нижче приводяться найбільш типові випадки
криволінійної регресії й формули розрахунків її параметрів:
а) параболічна залежність ![]() .
.
Параметри регресії a, b, c знаходяться з рішення системи:
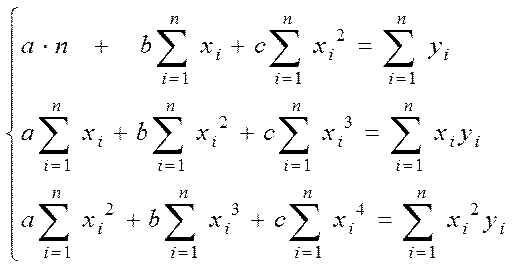 (5.13)
(5.13)
б) гіперболічна залежність 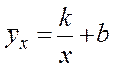 .
.
Робимо заміну 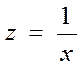 і
зводимо задачу до лінійної регресії
і
зводимо задачу до лінійної регресії ![]() . Параметри k
і b знаходяться за формулами лінійної регресії (з точністю до
позначень):
. Параметри k
і b знаходяться за формулами лінійної регресії (з точністю до
позначень):
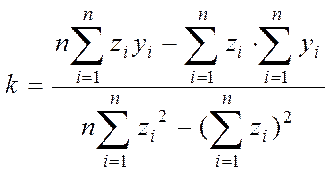 ,
,
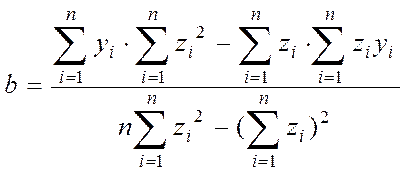 . (5.14)
. (5.14)
де 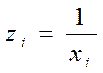 .
.
в) логарифмічна залежність ![]() .
.
Робимо заміну ![]() і
зводимо задачу до лінійної регресії
і
зводимо задачу до лінійної регресії ![]() .
.
Далі використовують формули (5.14).
д) експоненціальна залежність 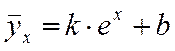 .
.
Робимо заміну z = ex і
зводимо задачу до лінійної регресії ![]() .
.
Далі використовують формули (5.14).
е) степенева залежність 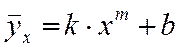
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.