Математична статистика в гірничо-геологічних розрахунках, страница 34

Рисунок 9.2

 

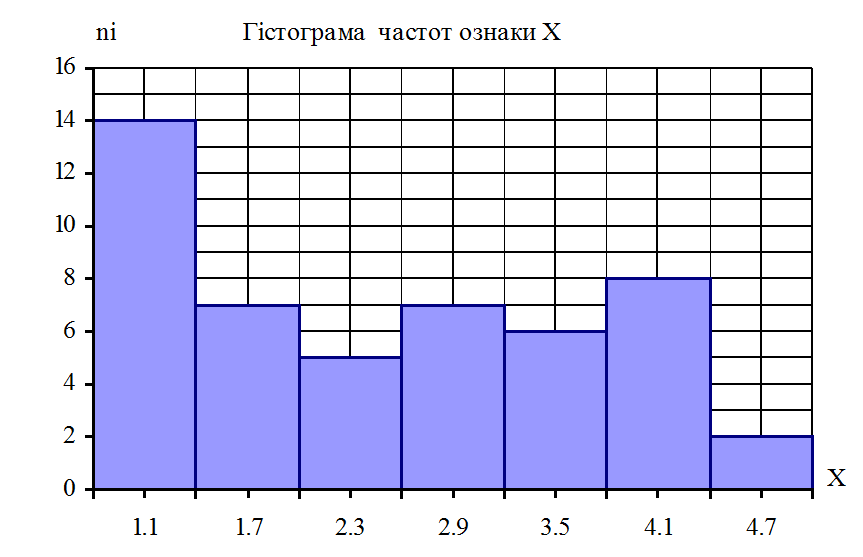Рисунок 9.3

 

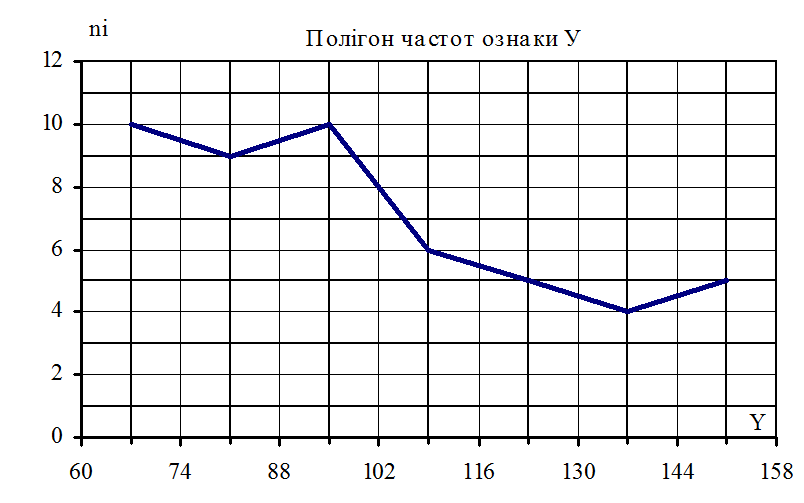Рисунок 9.4

 

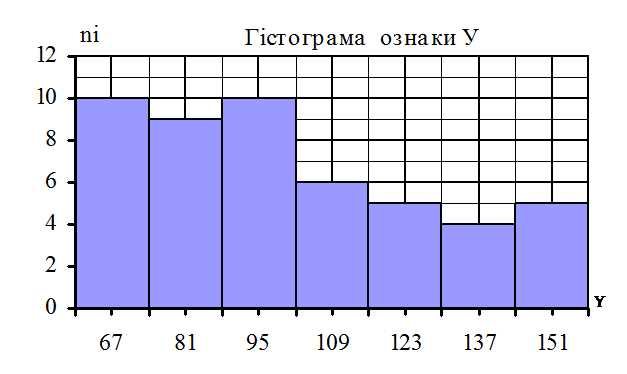Рисунок 9.5

3.   Визначити числові характеристики вибірок по кожній ознаці.

а)   Визначимо числові характеристики вибірки  ознаки Х.

Використовуємо метод “умовного нуля ”. Виберемо умовний нуль зі статистичного ряду ознаки : С = 2,9 .

Переходимо до умовних варіантів  по формулі: u_i = (x_i –C)/h, де h = 0,6.

Далі заповнюємо спеціальну таблицю.

i	інтервали	xi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	0,8 –1,4	1.1	14	-3	-42	126	56
2	1,4 -2	1.7	7	-2	-14	28	7
3	2 -2,6	2.3	5	-1	-5	5	0
4	2,6 - 3,2	2.9	7	0	0	0	7
5	3,2 - 3,6	3.5	6	1	6	6	24
6	3,6 - 4,4	4.1	8	2	16	32	72
7	4,4 - 5	4.7	2	3	6	18	32
Сума			49		-33	215	198

Для перевірки правильності обчислень використовуємо тотожність:

ån_i(u_i+1)² = ån_iu_i² + 2ån_iu_i + n

Одержимо: 198 = 215 + 2?(–33) + 49

198 = 198    – вірно.

З таблиці знаходимо умовні моменти:

М₁ = ån_iu_i / n = -33/49 = –0,6735

М₂ = ån_iu_i² / n = 198/49 = 4,3878;

Вибіркова середня дорівнює:

 = М₁·h + C =  –0,6735×0,6 + 2,9 = 2,50.

Вибіркова дисперсія дорівнює:

D_в = [M₂  - (M₁)²]·h² =  [4,3878 – (-0,6735)²]·0,6² = 1,4163.

Вибіркове середнє квадратичне відхилення дорівнює

.

Обчислимо виправлену вибіркову дисперсію

S ² = .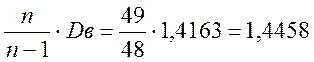

Обчислимо виправлене вибіркове середнє квадратичне відхилення:

 1,2024. Позначимо результат S _x = 1,2.

Отримані результати дозволяють зробити наступні висновки.

Середня швидкість посування очисного вибою по вибірці дорівнює 2,5 м/добу. Середній розкид швидкості посування очисного вибою навколо середньої по вибірці дорівнює 1,2 м/добу.

б)   аналогічно визначаємо числові характеристики вибірки ознаки У. Виберемо умовний нуль С = 109; h = 14.

i	інтервали	уi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	60 - 74	67	10	-3	-30	90	40
2	74 - 88	81	9	-2	-18	36	9
3	88-102	95	10	-1	-10	10	0
4	102-116	109	6	0	0	0	6
5	116-130	123	5	1	5	5	20
6	130-144	137	4	2	8	16	36
7	144-158	151	5	3	15	45	80
Сума			49		-30	202	191

Перевірка:  191 = 202 + 2·(–30) + 49 – вірно.

З таблиці знаходимо умовні моменти:

М₁ =  –30/49 = –0,6122;

М₂ = 202/49 = 4,1224;

Вибіркова середня дорівнює:  =  –0,6122×14 + 109 = 100,43

Вибіркова дисперсія дорівнює:

D_в = [M₂  - (M₁)²]·h² =  [4,1224 – (-0,6122)²]·14² = 734,5306

Вибіркове середнє квадратичне відхилення дорівнює

=27,1022.

S ² = ;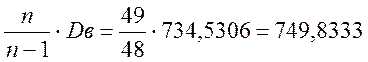

 27,383.

Позначимо результат S _у = 27,383 .

Отримані результати дозволяють зробити наступні висновки.

Середня величина опускання покрівлі по вибірці дорівнює 100,43 мм. Середній розкид величини опускання покрівлі  навколо середньої по вибірці дорівнює 27,383 мм.

4.  Перевіримо гіпотезу про нормальний розподіл ознаки Х.  Висунемо гіпотези:

1.   Н₀: Ознака Х підкоряється нормальному закону розподілу

2.   Н₁: Ознака Х не підкоряється нормальному закону розподілу

Для перевірки гіпотез використовуємо критерій Пірсона. За  вихідні дані беремо інтервальний ряд ознаки Х, отриманий у пункті 1 та  характеристики вибірки ознаки Х, знайдені в пункті 3: =2,5;    S_x =1,2.

Далі заповнимо таблицю за формулами:

z _i = (х _i – )/S_х;     z _i+1 = (х _i+1 – )/S_х.

Теоретичні частоти знайдемо по формулі:

n_i^*=n×[Ф(z_i+1) – Ф(z_i)],

де       функція Ф(z) обчислюється по таблиці (Додаток Б).

1	2	3	4	5	6	7	8	9	10	11	12
Х i	Х i+1	n i	z i	z i+1	Ф(z i)	Ф(zi+1)	ni*	N i*	N i	В i	V i
0.8	1.4	14	– ¥	-0,92	-0.5	-0.3203	8.8033	8.8033	14	3.0677	22.2644
1.4	2	7	-0.92	-0.42	-0.3203	-0.1615	7.7813	7.7813	7	0.0785	6.2971
2	2.6	5	-0.42	0.08	-0.1615	0.0332	9.5425	9.5425	5	2.1624	2.6198
2.6	3.2	7	0.08	0.58	0.0332	0.2202	9.1610	9.1610	7	0.5098	5.3488
3.2	3.8	6	0.58	1.08	0.2202	0.3607	6.8847	6.8847	6	0.1137	5.2290
3.8	4.4	8	1.08	1.58	0.3607	0.4433	4.0502	6.8272	10	1.4745	14.6473
4.4	5	2	1,58	+ ¥	0.4433	0.5000	2.7770
Разом		46					49		49	7.4065	56.4065