Гіпотеза – це висловлення можливого характеру. Під статистичною гіпотезою розуміють гіпотезу про вид розподілу генеральної сукупності або параметри розподілу генеральної сукупності.
Прикладами статистичних гіпотез є наступні висловлення: генеральна сукупність, що описує потужність пласта вугілля, має нормальний закон розподілу; генеральна середня (математичне сподівання потужності пласта) дорівнює 1 м.
Визначення. Статистична гіпотеза називається непараметричною, якщо в ній сформульовані припущення щодо виду функції розподілу.
Визначення. Статистична гіпотеза називається параметричною, якщо в ній сформульовані припущення щодо значень параметрів функції розподілу відомого виду.
Визначення. Нульовою гіпотезою називають основну гіпотезу і позначають символом Но. Звичайно нульові гіпотези затверджують, що розходження між порівнюваними величинами (параметрами чи функціями розподілу) відсутні, а відхилення, що спостерігаються, пояснюються лише випадковими коливаннями вибірки.
Визначення. Альтернативною (конкуруючою) називається гіпотеза, що конкурує з нульовою гіпотезою у тому розумінні, що якщо нульова гіпотеза відкидається, то приймається альтернативна, котру позначають символом Н1 .
Перевірку статистичних гіпотез звичайно здійснюють у наступному порядку:
а) Виходячи з вибіркових даних х1, х2, …, хn і керуючись конкретними умовами розглянутої задачі, формулюють основну гіпотезу Н0 і конкуруючу гіпотезу Н1 . Конкуруюча гіпотеза являє собою ту гіпотезу, що буде прийнята, якщо відкинуть основну гіпотезу.
б) Задаються імовірністю a, яку називають рівнем значущості помилки першого роду. Пояснимо її зміст. Рішення про те, чи можна вважати висловлення Н0 справедливим для генеральної сукупності, приймається по вибірковим даним, тобто по обмеженому ряді спостережень, отже, це рішення може бути помилковим. При цьому може мати місце помилка двох родів:
· відкидають гіпотезу Н0 чи, інакше, приймають альтернативну гіпотезу Н1, тоді як насправді гіпотеза Н0 вірна – це помилка першого роду;
· приймають гіпотезу Н0, тоді як насправді висловлення Н0 невірне, тобто вірною є гіпотеза Н1 – це помилка другого роду.
Виходить, рівень значущості a - це ймовірність помилки першого роду, тобто ймовірність того, що вірна основна гіпотеза буде відкинута і прийнята помилкова конкуруюча гіпотеза;
в) уводять статистичний критерій перевірки сформульованих гіпотез, котрий являє собою випадкову величину, яка підкоряється визначеному заздалегідь відомому закону розподілу, якщо вірна основна гіпотеза. За рівнем значущості помилки першого роду будують припустиму область (де приймається гіпотеза Н0) і критичну область (де відкидається гіпотеза Н0 і приймається гіпотеза Н1). Для побудови цих областей використовують критичні точки, які відокремлюють припустиму і критичну області.
д) за результатами вибірки визначають спостережуване значення статистичного критерію Ксп, і визначають область, у яку отримане значення критерію попадає. Якщо спостережуване значення критерію потрапляє в критичну область, то гіпотезу Н0 відкидають і приймають гіпотезу Н1. Якщо спостережуване значення критерію потрапляє в припустиму область, то говорять, що немає підстав відкинути гіпотезу Н0 . Висловлюючись простіше (але не точніше), це означає, що гіпотеза Н0 приймається.
У математичній статистиці вивчена безліч різних гіпотез, кожна з яких перевіряється своїм способом. Розглянемо деякі з них, що найбільше зустрічаються в гірничо-геологічних статистичних розрахунках.
Маємо параметри вибірок
за ознакою Х: n1 – обсяг вибірки;
Sx2 – виправлена вибіркова дисперсія;
за ознакою У: n2 – обсяг вибірки;
Sу2 – виправлена вибіркова дисперсія.
Нехай для визначеності Sx2 > Sу2.
Потрібно при заданому рівні значущості a порівняти дисперсії D(X) і D(Y) генеральних сукупностей.
Висунемо основну й альтернативну гіпотези. Розглянемо два випадки:
a) Н0: D(Х) = D(У) б) Н0: D(Х) = D(У)
Н1: D(Х) > D(У) Н1: D(Х) ¹ D(У)
Для перевірки гіпотез за результатами вибірок обчислюємо спостережуване значення критерію (відношення більшої дисперсії до меншої):
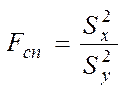
Цей критерій є випадковою величиною, що підкоряється закону розподілу Фішера–Снедекора.
Критичні області і точки залежать від висунутих альтернативних гіпотез H1 .
а) Н1: D(Х) > D(У)
Критична область є правобічною. Критична точка знаходиться за таблицею критичних точок розподілу Фишера–Снедекора (Додаток И)
Fкр=F(a; k1; k2),
де a – заданий рівень значущості;
k1 = n1 –1 – число степенів вільності більшої виправленої дисперсії (Sx2);
k2 = n2 –1 – число степенів вільності меншої виправленої дисперсії (Sy2).
Якщо в результаті порівняння виявиться Fсп < Fкр, то немає підстав відкинути нульову гіпотезу H0; якщо ж Fсп > Fкр , те нульова гіпотеза H0 відкидається; приймається гіпотеза H1;
б) Н1: D(Х) ¹ D(У)
Критична область є двосторонньою. Критична точка знаходиться за таблицею критичних точок розподілу Фишера – Снедекора (Додаток И)
Fкр=F(a/2; k1; k2),
де a – заданий рівень значущості;
k1 = n1 –1 - число степенів вільності більшої виправленої дисперсії (Sx2);
k2 = n2 –1 - число степенів вільності меншої виправленої дисперсії (Sy2).
Якщо в результаті порівняння Fсп < Fкр, то немає підстав відкинути нульову гіпотезу H0; якщо ж Fсп > Fкр , то нульова гіпотеза H0 відкидається; приймається гіпотеза H1.
Маємо параметри вибірок
за ознакою Х: n1 – обсяг вибірки;
![]() – вибіркова середня;
– вибіркова середня;
Sx2 – виправлена вибіркова дисперсія;
за ознакою У: n2 – обсяг вибірки;
![]() – вибіркова середня;
– вибіркова середня;
Sу2 – виправлена вибіркова дисперсія.
Потрібно при заданому рівні значущості a порівняти математичні сподівання М(Х) і М(У) генеральних сукупностей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.