Математична статистика в гірничо-геологічних розрахунках, страница 10

е) За таблицею критичних точок (Додаток Е) знаходять критичне значення критерію

χ²_кр = χ² (a ; k);

ж) Якщо в результаті порівняння виявиться χ²_сп < χ²_кр, то немає підстав відкинути нульову гіпотезу H₀; якщо ж χ²_сп > χ²_кр, то нульова гіпотеза H₀ відкидається; приймається гіпотеза H₁.

4.5    Перевірка гіпотези про вид розподілу генеральної сукупності за критерієм Колмогорова-Смирнова

Нехай емпіричний розподіл задається інтервальним статистичним рядом

Інтервал	х 1 – х 2	х 2 – х 3	…	х i–1 – х i	…	х m –1 – х m
ni	n 1	n 2	…	n i	…	n m

Обсяг вибірки дорівнює n = n ₁+ n ₂+…+n_m .

Потрібно при заданому рівні значущості a перевірити, чи підкоряється генеральна сукупність обраному теоретичному закону розподілу f(x).

Висунемо гіпотези:

Н₀: Ознака Х підкоряється закону розподілу f(x).

Н₁: Ознака Х не підкоряється закону розподілу f(x).

Для перевірки сформульованих гіпотез за допомогою критерію Колмогорова-Смирнова необхідно виконати ряд розрахунків:

а)   визначають по вибірці параметри обраного теоретичного розподілу f(x). Нехай r - число параметрів розподілу;

б)   для кожного інтервалу Х визначають імовірності влучення ознаки Х в даний інтервал. Для цього потрібно використовувати формулу з теорії ймовірності

.

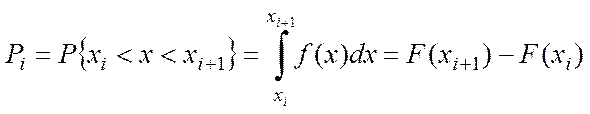Тут    f(x) – диференціальна функція розподілу,

F(x) – інтегральна функція розподілу. Для багатьох видів розподілу маються таблиці значень f(x) і F(x).

в)   визначають теоретичні частоти

.

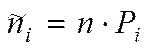д)   знаходять накопичені частоти. Позначимо їх для емпіричних частот як n×F_n(x) ; для теоретичних частот – n×F(x). Для знаходження накопичених частот потрібно для кожного інтервалу послідовно складати частоти, починаючи з першого інтервалу і закінчуючи поточним інтервалом. Результати розрахунків зручно записати в таблицю;

е)   далі обчислюють модуль різниці накопичених частот у кожнім інтервалі

ôn×F_n(x) – n×F(x)ô = n×ôF_n(x) –F(x)ô.

ж)  знаходять найбільший з отриманих модулів

n ×D = max{n×ôF_n(x) – F(x)ô}.

и)  визначають спостережуване значення критерію згоди Колмогорова-Смірнова

.

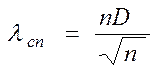Цей критерій є випадковою величиною, що підкоряється закону розподілу Колмогорова;

к)   за таблицею критичних точок (Додаток К), використовуючи заданий рівень значущості a, знаходять критичне значення критерію l_кр = l(a);

л)   якщо в результаті порівняння виявиться l_сп < l_кр, то немає підстав відкинути нульову гіпотезу H₀; якщо ж l_сп > l_кр, то нульова гіпотеза H₀ відкидається; приймається гіпотеза H₁.

Зауваження: у критерії Колмогорова –Смирнова рекомендується брати більш “твердий” рівень значущості (a ³ 0,1), ніж при використанні критерію Пірсона.

4.6    Приклади з перевірки статистичних гіпотез

Приклад 1.

Передбачається, що застосування нової технології в розробці пластових родовищ приведе до збільшення якості вугілля. Результати контролю з якості добутого вугілля двома бригадами, що працюють в аналогічних умовах, але використовують різні технології, приведені нижче. Виміри велися за відсотком засмічення вугілля, вироблюваного однією бригадою за зміну за старою технологією (ознака Х₁) і за нової технології (ознака Х₂).

Х₁ ( %): 13; 10,5; 11; 12; 20; 18,8; 10

 Х₂ ( %): 6; 13; 21; 7; 9; 9; 5; 10

Чи підтверджують ці результати припущення про ефективність застосування нової технології? Прийняти a = 0,01 .

Припустити, що вибірки отримані з нормально розподілених генеральних сукупностей.

Проведемо первинну обробку статистичних даних, використовуючи формули для незгрупованого ряду даних (розділ 2.1).

Одержимо по ознаці Х₁ : обсяг вибірки n=7;

Вибіркова середня (13+10,5+11+12+20+18,8+10)/7= 13,61;

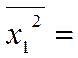 (13²+10,5²+11²+12²+20²+18,8²+10²)/7= 199,67;

Вибіркова дисперсія D_в = 199,67 –13,61² = 14,44;

Виправлена СКВ   S²_x1 =14,44×7/6 = 16,84.

Параметри ознаки Х₂ розраховуються аналогічно:

n=8;  10; 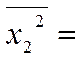 116,625 ;

D_в = 116,625 – 10² = 16,625 : S²_x2 =16,625×8/7 = 19 .

Питання ефективності застосування нової технології зводиться до перевірки статистичної гіпотези про рівність двох середніх (математичних сподівань) генеральних сукупностей. Для коректного рішення необхідно переконатися в рівності дисперсій зазначених генеральних сукупностей (п. 4.1).

Висунемо основну й альтернативну гіпотези.

Н₀: D(Х₂) = D(Х₁)

Н₁: D(Х₂) > D(Х₁)

Для перевірки гіпотез за результатами вибірок обчислюємо спостережуване значення критерію (відношення більшої дисперсії до меншої):

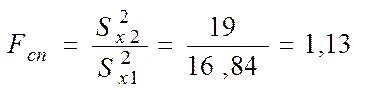
Критична область є правобічною. Критична точка знаходиться за таблицею критичних точок розподілу Фішера – Снедекора (Додаток И).

При a =0,01; k₁ = 8 –1 = 7; k₂ = 7 –1 = 6 маємо:

F_кр= F(0,01; 7; 6) = 8,26

Після порівняння одержимо F_сп < F_кр. Виходить, немає підстав відкинути нульову гіпотезу H₀. Отже, приймаємо гіпотезу про рівність дисперсій двох генеральних сукупностей.

Для з'ясування ефективності застосування нової технології перевіримо статистичну гіпотезу про рівність двох середніх генеральних сукупностей (п.4.2).

Висунемо основну й альтернативну гіпотези:

Н₀: M(Х₁) = M(Х₂).

Н₁: M(Х₁) > M(Х₁).

Прийняття нульової гіпотези Н₀ дасть підстави вважати, що нова система технології видобутку вугілля не приводить до зміни засмічення вугілля.

Прийняття гіпотези H₁ буде значити, що нова система технології приводить до зменшення засмічення вугілля, і, отже, вона ефективна.

Для перевірки гіпотез за результатами вибірок обчислюємо спостережуване значення критерію

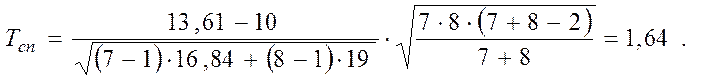
Цей критерій є випадковою величиною, що підкоряється закону розподілу Стьюдента з k =7+8–2=13 степенями вільності.

Критична область є правобічною. Критична точка знаходиться за таблицею критичних точок розподілу Стьюдента (Додаток Ж, однобічна критична область)

t_кр = t(0,01; 13) = 2,65.

Після порівняння одержимо T_сп < t_кр . Виходить, немає підстав відкинути нульову гіпотезу H₀. Таким чином, нова система технології не приводить до зміни якості вугілля по засміченню. Вона не ефективна.

Приклад 2