Математична статистика в гірничо-геологічних розрахунках, страница 33

Зробити прогноз при Х =90 кгс/см².

9.4  Приклад виконання контрольної роботи зі статистики для студентів заочної форми навчання

ЗАВДАННЯ. В нижченаведеній таблиці зібрані дані по ряду шахт.

Позначення:     Х – швидкість посування очисного вибою, м/добу;

У – величина опускання покрівлі, мм.

Х	0,8	0,8	1	1	1	1,2	1,2	1,2	1,2	1,4
У	140	154	124	140	154	124	134	146	158	104
Х	1,4	1,4	1,4	1,4	1,6	1,6	1,6	1,8	2	2
У	114	124	134	146	82	102	126	114	94	106
Х	2	2,2	2,2	2,4	2,4	2,6	2,8	2,8	2,8	3
У	124	76	108	84	96	88	74	94	104	86
Х	3,2	3,2	3,6	3,6	3,6	4	4	4,4	4,4	4,8
У	74	96	64	74	96	62	84	66	94	80
Х	3,1	3,6	3,5	3,3	4,1	4	4,4	4,4	4,8	0,1
У	99	65	68	96	60	84	60	94	79	100

Для приведених статистичних даних виконати  розрахунок у наступній послідовності:

1.  Провести первинну обробку статистичних даних, включаючи перевірку даних. Результати представити у виді таблиць. Побудувати статистичні ряди для кожної ознаки.

2.  Побудувати гістограму і полігон частот (чи відносних частот) по кожній ознаці.

3.  Використовуючи метод “умовного нуля”, визначити числові характеристики вибірок по кожній ознаці: вибіркове середнє; вибіркову дисперсію; виправлену вибіркову дисперсію; виправлене вибіркове середнє квадратичне відхилення. Дати пояснення результатам.

4.  При заданому рівні значимості a=0,05 перевірити гіпотезу про нормальний закон розподілу генеральних сукупностей по ознаці Х чи ознаці У.

5.  Для ознак X і Y побудувати кореляційне поле і дати попередній аналіз залежності між ознаками.

6.  Визначити параметри рівняння лінійної регресії.

7.  Визначити коефіцієнт кореляції і перевірити його на значущість. Знайти коефіцієнт детермінації. Зробити висновок про наявність зв'язку між ознаками, використовуючи шкалу Чедока.

8.  Побудувати отриману лінію регресії.

9.  Визначити абсолютну і відносну похибки рівняння лінійної
регресії.

10.   Використовуючи отримане рівняння регресії, дати точковий прогноз  по ознаці У при заданому значенні ознаки X =1,5 м.

Зразок виконання завдання

1.   Рішення задачі почнемо з перевірки вихідних даних. Побудуємо кореляційне поле (Рис. 9.1), у якому  представлено 50 точок (обсяг вибірки n = 50).

З побудованої діаграми бачимо, що одна точка А (Х= 0,1 м/добу ; У= 100 мм)  “вискакує” із загальної сукупності. Проаналізуємо координати цієї точки:

0,1 м/добу – це означає 10 см посування очисного вибою на добу. При цьому величина опускання покрівлі дорівнює 100 мм. Ясно, що цього не може бути. Отже, спостереження Х= 0,1 м/добу ; У= 100 мм  вважаємо помилковим, і вилучаємо його із вибірки. Таким чином,  обсяг вибірки на цьому етапі приймається n = 49.

Викид

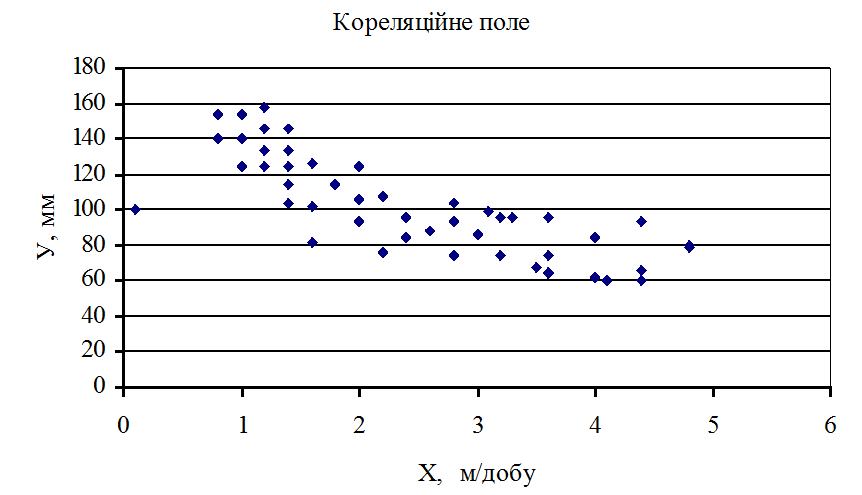
Рисунок 9.1

Почнемо первинну обробку статистичних даних.

а)   для ознаки Х визначимо найбільше і найменше значення ознаки:

X_min=0,8 ;    X_max=4,8;     обсяг вибірки  n = 49.

Число інтервалів розбивки визначимо за формулою Стерджеса:

k =1 + 3,322× lg n =  1 + 3,322× lg 49 = 6,61 » 7.

Знайдемо крок розбивки  h = (Х_max – X_min) / k..

У даному випадку  h = (4,8 – 0,8) / 7 = 0,6.

Зробимо групування даних для ознаки  Х.  Для цього підрахуємо, скільки значень ознаки Х  потрапить у кожний з інтервалів розбивки.

Результати групування заносимо в табл.9.1, що являє собою статистичний ряд по ознаці Х.

Таблиця 9.1

Інтервал	0,8 –1,4	1,4 – 2	2 – 2,6	2,6 – 3,2	3,2 – 3,6	3,6 – 4,4	4,4 – 5
Середина інтервалу хi	1,1	1,7	2,3	2,9	3,5	4,1	4,7
Частота  ni	14	7	5	7	6	8	2

Перевірка:14+7+5+7+6+8+2=49. Вірно.

б)   для ознаки У визначимо найбільше і найменше значення ознаки:

У_min=60 ;     У_мах=158;    обсяг вибірки n = 49.

Знайдемо крок розбивки h = (У_мах – У_min) / k.

У даному випадку h = (158 –60 )/ 7 = 14.

Зробимо групування даних для ознаки У. Результати групування заносимо в табл.9.2, що являє собою статистичний ряд по ознаці У.

Таблиця 9.2

Інтервал	60-74	74-88	88-102	102-116	116-130	130-144	144-158
y  i	67	81	95	109	123	137	151
ni	10	9	10	6	5	4	5

Перевірка: 10+9+10+6+5+4+5=49. Вірно.

2. 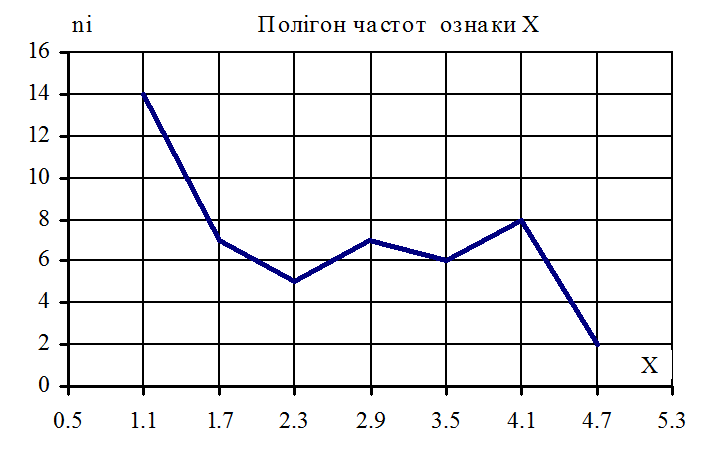 Побудуємо полігон і гістограму частот по ознакам Х та У. Відмітимо, що при спрощенім аналізі можна будувати гістограму по частотам n_i . Це не дуже точне трактування гістограми як емпіричної щільності розподілу, але  воно просте  при обчислюванні й побудові та характеризує щільність розподілу признака с точністю до сталого множника.