Математична статистика в гірничо-геологічних розрахунках, страница 11

При рівні значимості a = 0,05, використовуючи критерій згоди Пірсона, перевірити гіпотезу про нормальний закон розподілу генеральної сукупності ознаки У із задачі 1 (завдання 5).

Перевіримо гіпотезу про нормальний розподіл ознаки Y, використовуючи критерій Пірсона. Нормальний закон розподілу є двопараметричним розподілом з параметрами а (генеральна середня) і s (генеральне СКВ). Виходить, число r = 2. З вибірки по У візьмемо оцінки параметрів розподілу:

а »  =7,285; s » S _у = 2,254 .

Для кожного інтервалу ознаки У необхідно обчислити ймовірності потрапляння ознаки в даний інтервал. Використовуємо готову формулу з теорії ймовірності для величини, розподіленої нормально:

 .

Тут записана нормована нормальна випадкова величина

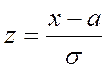. Функція Лапласа Ф(z )обчислюється за таблицею (Додаток Б). При цьому враховуємо, що Ф(–z) = – Ф(z); Ф(– ¥) = –0,5 ; Ф(+ ¥) = 0,5 .

У даному випадку замість випадкової величини Х беремо величину У. Далі заповнимо таблицю за формулами:

;

,

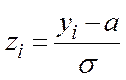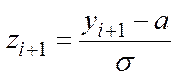причому крайню ліву точку інтервалу заміняємо на – ¥ ; крайню праву точку заміняємо на + ¥, оскільки теоретичний нормальний розподіл визначений на всій числовій осі від – ¥ до + ¥ .

Теоретичні частоти знайдемо за формулою:

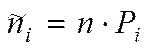
Заповнимо таблицю:

1	2	3	4	5	6	7	8	9	10	11	12
Уi	Уi+1	ni	zi	zi+1	Ф(zi)	Ф(zi+1)	ni*	Ni*	Ni	Вi	Vi
3,2	4,68	5	– ¥	-1,16	-0,5	-0,377	6,15	6,15	5	0,21504	4,06504
4,68	6,16	12	-1,16	-0,50	-0,377	-0,1915	9,28	9,28	12	0,80061	15,5256
6,16	7,64	14	-0,50	0,16	-0,1915	0,0636	12,76	12,76	14	0,12152	15,3665
7,64	9,12	10	0,16	0,81	0,0636	0,291	11,37	11,37	10	0,16507	8,79507
9,12	10,6	4	0,81	1,47	0,291	0,4292	6,91	10,45	9	0,2012	7,7512
10,6	12,08	3	1,47	2,13	0,4292	0,4834	2,71
12,08	13,56	2	2,13	+ ¥	0,4834	0,5	0,83
Сума		50								1,5034	51,5034

Після заповнення 8-го стовпця відзначаємо, що два останніх елементи в цьому стовпці менше п'яти. Оскільки в критерії Пірсона потрібно, щоб у кожнім інтервалі було не менше п'яти одиниць, то об'єднаємо частоти трьох останніх інтервалів N_i^* – для 8-го стовпця; N_i – для 3-го стовпці.

11-ий стовпець заповнюємо за формулою:

В_i =.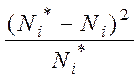

12-ий стовпець – контрольний. Він обчислюється за формулою:

V_i =.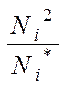

Зробимо перевірку: 50 + 1,5034 = 51, 5034. Вірно.

Зазначимо, що в результаті перевірки значення правої і лівої частин можуть відрізняться незначним образом.

Запишемо спостережуване значення критерію c²_сп =1,5034.

Виберемо рівень значущості помилки a=0,05.

Число степенів вільності дорівнює k=m –2 – 1 , де m – число інтервалів після об'єднання. У нашому випадку число інтервалів після об'єднання m= 5. Тоді число степенів вільності дорівнює k=5–3 = 2. Із таблиці критичних точок критерію c² (Додаток Е) знаходимо c²_кр(0,05; 2)=6.

Порівнюємо:                   c²_сп < c²_кр.

Отже, немає підстав відкинути гіпотезу про нормальний закон розподілу ознаки Y. Тому приймається гіпотеза про нормальний розподіл ознаки У.

Приклад 3. У результаті досліджень отримані дані за часом безвідмовної роботи стопора шляхового ( у годинах).

762	240	290	150	166	206	908	110	256	299
286	110	190	106	110	112	200	250	230	142
119	134	187	215	320	502	1246	340	365	314
390	412	473	114	596	807	220	1045	350	850

При рівні значущості a=0,2 за допомогою критерію Колмогорова-Смирнова перевірити гіпотезу про показниковий закон розподілу генеральної сукупності за часом безвідмовної роботи стопора.

Нехай ознака Х позначає час безвідмовної роботи стопора. Визначимо найбільше і найменше значення ознаки:

X_min=106 ;        X_max=1246 ;  обсяг вибірки n = 40.

Число інтервалів розбивки визначимо за формулою Стерджеса:

k =1 + 3,322× lg 40 = 6,3 .

Знайдемо крок розбивки h = (Х_max – X_min) / k.

У даному випадку h = (1246 –106) / 6,3 = 180,32. Приймемо h = 200.

Зробимо групування даних для ознаки Х.

Результати групування представимо в таблиці та розрахуємо параметри вибірки методом “умовного нуля”. Умовний нуль: С=600.

i	інтервали	хi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	100-300	200	24	-2	-48	96	24
2	300-500	400	6	-1	-6	6	0
3	500-700	600	4	0	0	0	4
4	700-900	800	3	1	3	3	12
5	900-1100	1000	2	2	4	8	18
7	1100-1300	1200	1	3	3	9	16
S			40		-44	122	74