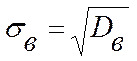Математична статистика в гірничо-геологічних розрахунках, страница 6

.

Виправлена вибіркова дисперсія:

.

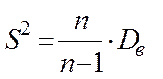Виправлене вибіркове середнє квадратичне відхилення:

.

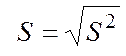Вибіркова асиметрія:

.

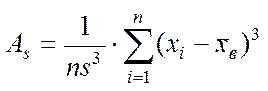Вибірковий ексцес:

.

2.2  Статистичні дискретні та інтервальні ряди

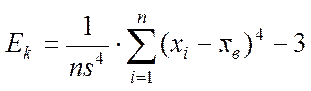Нехай вибірка задана дискретним статистичним рядом:

х i	х 1	х 2	…	х i	…	х k
ni	n 1	n 2	…	n i	…	n k

У цьому випадку розрахункові формули мають вид:

 ,

,

 , ,  ,

, .

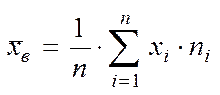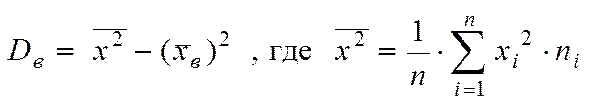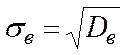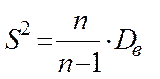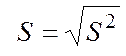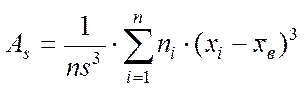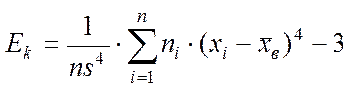Мода М_о при дискретному ряді дорівнює тому значенню варіанти х_m, якому відповідає найбільша частота n_m.

Медіана М_е розраховується по варіаційному (відсортованому) ряду так: якщо обсяг вибірки – непарне число n=2m+1, то медіана дорівнює варіанті з номером m+1 у цьому відсортованому ряді, тобто М_е=х_m+1 ; якщо ж обсяг вибірки – парне число n=2m, то медіана дорівнює середньому арифметичному із двох центральних варіант, тобто М_е=0,5×(х_m + х_m+1).

Якщо вибірка задана інтервальним статистичним рядом

Інтервал	х 1 – х 2	х 2 – х 3	…	х i–1 – х i	…	х k –1 – х k
ni	n 1	n 2	…	n i	…	n k

то в цьому випадку заміняють інтервали їхніми серединами і використовують формули для дискретного ряду.

На відміну від дискретних рядів визначення моди і медіани вимагає проведення спеціальних розрахунків.

Мода обчислюється за формулою:

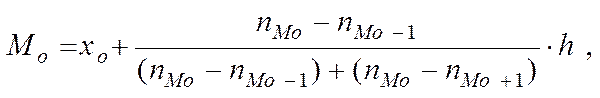
де       х₀ – початок модального інтервалу;

n_Mo– частота модального інтервалу;

n_{Mo -1}– частота інтервалу, що передує модальному;

n_{Mo +1}– частота наступного за модальним інтервалу;

h – величина модального інтервалу.

Медіанаобчислюється за формулою:

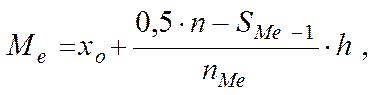
де       х₀ – початок медіанного інтервалу;

n_Mе– частота медіанного інтервалу;

n – обсяг вибірки;

S_{Me -1}– накопичена частота інтервалу, що передує медіанному;

h – величина медіанного інтервалу.

2.3 Метод “умовного нуля”

Якщо вибірка представлена статистичним рядом із рівновіддаленими варіантами чи інтервальним статистичним рядом з рівними інтервалами розбивки, то доцільно для спрощення розрахунків використовувати метод “умовного нуля”. У цьому випадку вибирають у якості “умовного нуля” одну із варіант С, що стоїть в центрі ряду і має найбільшу частоту. Потім переходять до умовних варіант за формулою
u_i = (x_i –C)/h і заповнюють спеціальну таблицю.

i	Інтервали	Середина xi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1
2
…
Сума			S		S	S	S

Для перевірки правильності обчислень використовується тотожність:

ån_i(u_i+1)² = ån_iu_i² + 2ån_iu_i + n .

Із таблиці знаходяться умовні моменти:

М₁ = ån_iu_i / n ;  М₂ = ån_iu_i² / n .

Вибіркова середня дорівнює:  = М₁·h + C

Вибіркова дисперсія дорівнює:

D_в = [M₂ - (M₁)²] ·h² .

Далі знаходять інші оцінки за тими ж формулами, що і раніш:

 , ,  .

2.4 Задача 1. Точкові оцінки

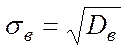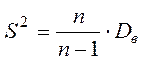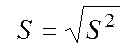Як приклад розрахунків оцінок параметрів розподілу продовжимо рішення задачі 1, завдання 3.

Визначимо числові характеристики вибірки за ознакою Х.

Виберемо зі статистичного ряду ознаки Х (табл. 1.4) умовний нуль С = 1,2.

Переходимо до умовних варіантів за формулою: u_i = (x_i –1,2)/h, де h = 0,1. Далі заповнюємо спеціальну таблицю.

i	Інтервали	xi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	0,85-0,95	0,9	6	-3	-18	54	24
2	0,95-1,05	1	7	-2	-14	28	7
3	1,05-1,15	1,1	20	-1	-20	20	0
4	1,15-1,25	1,2	6	0	0	0	6
5	1,25-1,35	1,3	5	1	5	5	20
6	1,35-1,45	1,4	3	2	6	12	27
7	1,45-1,55	1,5	3	3	9	27	48
			50		-32	146	132

Для перевірки правильності обчислень використовуємо тотожність:

ån_i(u_i+1)² = ån_iu_i² + 2ån_iu_i + n

Підставляючи з таблиці значення сум, маємо:

132 = 146 + 2·(–32) + 50. Вірно.

З таблиці знаходимо умовні моменти:

М₁ = ån_iu_i / n = -32/50 = –0,64;

М₂ = ån_iu_i² / n = 146/50 = 2,92;

Вибіркова середня дорівнює:

 =М₁·h +C = –0,64×0,1+1,2= 1,136.

Вибіркова дисперсія дорівнює:

D_в = [M₂ - (M₁)²]·h² = [2,92 – (-0,64²]·0,1² = 0,025104

Вибіркове середнє квадратичне відхилення дорівнює

 0,158442

Обчислимо виправлену вибіркову дисперсію

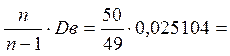S ² =  0,02562 ;

Обчислимо виправлене вибіркове середнє квадратичне відхилення:

 0,160. Позначимо результат S _x = 0,160.

Отримані результати дозволяють зробити наступні висновки.

Середня потужність пласта по вибірці дорівнює 1,14 м. Середній розкид потужності пласта навколо середньої по вибірці дорівнює 0,16 м.

Аналогічно визначаємо числові характеристики вибірки за ознакою У. Виберемо умовний нуль С = 8,38 ; h = 1,48.

i	інтервали	уi	ni	ui	ni× ui	ni× ui2	ni× (ui + 1)2
1	3,2 - 4,68	3,94	5	-3	-15	45	20
2	4,68 - 6,16	5,42	12	-2	-24	48	12
3	6,16 - 7,64	6,9	14	-1	-14	14	0
4	7,64 - 9,12	8,38	10	0	0	0	10
5	9,12 - 10,6	9,86	4	1	4	4	16
6	10,6 -12,08	11,34	3	2	6	12	27
7	12,08 -13,56	12,82	2	3	6	18	32
разом			50		-37	141	117