Математична статистика в гірничо-геологічних розрахунках, страница 14

Робимо заміну z = x^m і зводимо задачу до лінійної регресії .

Далі використовують формули (5.14).

Тіснота зв'язку між результативною ознакою Х и фактором У при нелінійній формі їхнього зв'язку оцінюється за допомогою коефіцієнта детермінації R², що знаходиться за тією ж формулою (5.11) з п.5.6, що і для лінійного зв'язку. Якісна оцінка тісноти зв'язку робиться за шкалою Чедока.

Аналогом коефіцієнта кореляції для нелінійного випадку служить кореляційне відношення  .

5.8    Множинна регресія

Оскільки в гірничій справі важливі виробничі показники найчастіше пояснюються багатьма факторами, то для їхнього прогнозу застосовується множинна регресія, параметри якої визначаються також по методу найменших квадратів.

Загальний вид моделі: ,

де х₁, х₂, …, х_k – незалежні фактори, а у – результуючий показник. При цьому функція множинної регресії  може бути як лінійна, так і нелінійна.

Дуже важливими є питання про те, скільки незалежних факторів може бути в рівнянні множинної регресії при заданому обсязі вибірки n. Звичайно використовують таке правило: число спостережень повинне бути не менш чим у 8-10 разів більше числа факторів у рівнянні регресії.

          Найбільш зручна форма розрахунку лінійної множинної регресії – матрична. Приведемо розрахункові формули, які можна легко реалізувати в комп'ютері за допомогою пакета програм Mathcad.

Нехай шукане рівняння регресії має вид:

 .

Уведемо матрицю оцінок параметрів регресії

.

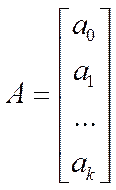Ця матриця складається з невідомих параметрів, які будуть оцінюватись надалі відповідними оцінками. Для складання рівняння регресії візьмемо вибірку обсягу n і запишемо спостережувані значення ознак : Х₁, Х₂…,Х_k та У.

На підставі отриманих даних сформуємо матриці:

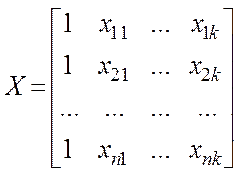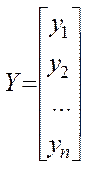, . Тут х_ij означає спостережуване значення j - ої ознаки для i -го спостереження.

У матричній формі рівняння регресії має вид: Х×А = У

Помножимо обох частин рівняння ліворуч на транспоновану матрицю Х^Т.

Одержимо: Х^Т×Х×А = Х^Т ×У. Позначимо матрицю моментів У = Х^Т×Х. Тоді з матричного рівняння В×А = Х^Т ×У можна знайти шукану матрицю оцінок:

А = В^–1 × (Х^Т ×У).

Розрахунок коефіцієнта детермінації здійснюється за формулою:

.

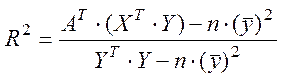Кореляційне відношення обчислюється за формулою  .

Перевірка моделі на адекватність здійснюється за критерієм Фішера:

,

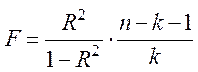де       n – обсяг вибірки,

k – число змінних у рівнянні регресії.

Потім за таблицею критичних точок розподілу Фішера – Снедекора

(Додаток И) знаходимо критичне значення критерію

F_кр = F(a , k₁ , k₂),

де       a - значущість помилки першого роду;

k₁ = k ;

k₂ = n – k –1.

Якщо спостережуване значення критерію F виявиться більше критичного, то визнаємо отриману множинну регресію адекватною; якщо спостережуване значення критерію F виявиться менше критичного, то робимо висновок, що побудована модель не адекватна реальної.

Зауваження 1 Даний спосіб перевірки моделі на адекватність можна застосовувати і для одномірних як лінійних, так і нелінійних моделей.

Зауваження 2 Матричний підхід у складанні рівняння регресії можна також використовувати для випадку лінійної регресії з однією перемінною.

Розглянемо приклад складання множинної регресії.

Задача. Досліджується залежність місячного видобутку вугілля по ділянці від потужності розроблювального пласта і глибини проведення робіт.

Уведемо позначення факторів: У – місячний видобуток вугілля; Х₁ – потужність пласту, Х₂ – глибина проведення робіт.

Використовуючи фізичну сутність факторів, визначимо залежні і незалежні ознаки:               результативна (залежна) ознака – У ;

незалежні ознаки – Х₁ і Х₂ .

Вихідні дані по 20 лавам, що працюють приблизно в однакових умовах, приводяться в таблиці:

i	Y, тис.тонн	X1 , м	X2 , м
1	22,260	1,37	1080
2	27,608	1,11	698
3	14,056	0,96	895
4	22,288	1,45	400
5	21,420	1,56	952
6	25,088	1,21	550
7	56,588	1,49	402
8	31,530	1,1	406
9	35,240	1,2	508
10	29,764	1,25	480
11	21,224	1,16	730
12	23,856	1,05	450
13	46,270	1,52	420
14	19,292	0,91	750
15	10,332	0,85	1560
16	13,972	0,92	1060
17	26,656	1,1	490
18	16,744	1,05	762
19	24,360	0,96	460
20	38,640	1,33	545

У даній задачі обсяг вибірки дорівнює n = 20.

Число незалежних змінних дорівнює k = 2.

Рівняння лінійної регресії має вид:

Розрахунки здійснимо за допомогою пакета програм Mathcad.

Реалізація розрахунків усіх необхідних параметрів і характеристик даної задачі в середовищі Mathcad демонструється нижче:

          

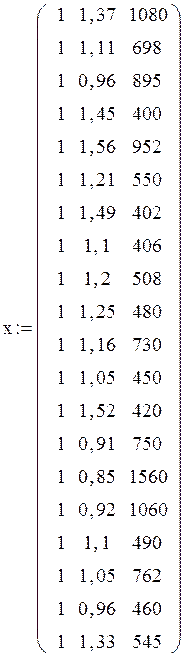
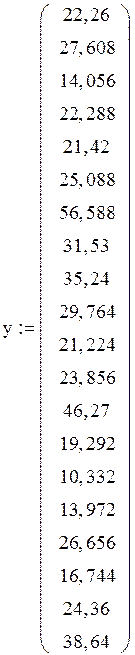
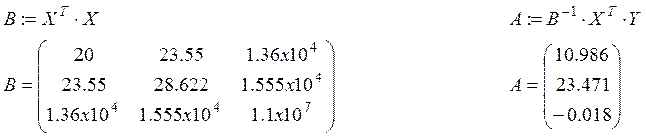
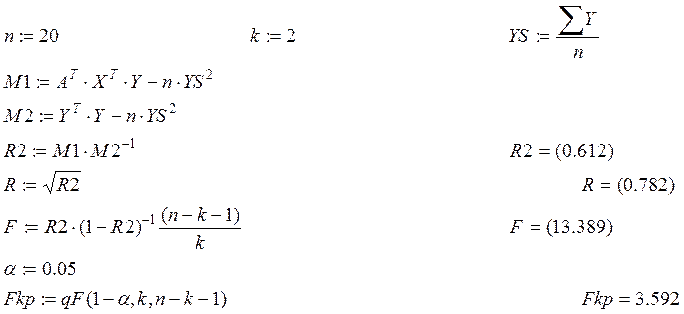
Використовуючи результати розрахунків, зробимо висновки.

1)   Рівняння лінійної регресії має вид:

.

Виходить, зі збільшенням потужності пласта (Х₁) місячний видобуток вугілля збільшується, а зі збільшенням глибини робіт (Х₂) місячний видобуток вугілля зменшується.

2)   Коефіцієнт детермінації дорівнює R² = 0,612. Отже, варіації ознак Х₁ і Х₂ пояснюють 61,2% загальної дисперсії результативної ознаки У. Інша частина дисперсії В (38,8%) пояснюється іншими факторами, неврахованими в даній моделі. Користаючись шкалою Чедока, можна стверджувати, що між місячним видобутком вугілля і незалежними факторами, такими як потужність пласта і глибина проведення робіт існує помітний зв'язок.

3)   Кореляційне відношення для лінійної множинної моделі дорівнює

R = 0,782.