Математична статистика в гірничо-геологічних розрахунках, страница 16

З останнього рядка одержимо:

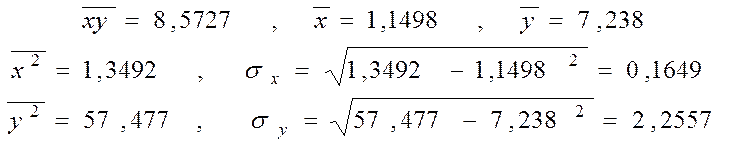
Підставивши у формулу (5.5) пункту 5.4, отримаємо:

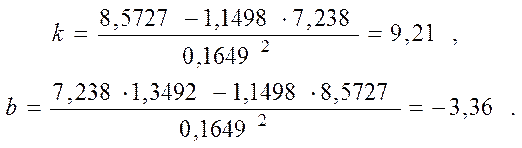
Зробимо перевірку:  Вірно.

Отже, рівняння лінійної регресії має вид :

 = 9,21×х – 3,36

Завдання 9. Визначимо вибірковий коефіцієнт кореляції за формулою

.

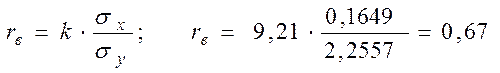Перевіримо коефіцієнт кореляції на значущість.

Висунемо гіпотези:     Основна гіпотеза               H ₀ :, r_г = 0

Конкуруюча гіпотеза        H ₁ : r_г ¹ 0.

Для перевірки гіпотези H ₀ обчислимо спостережуване значення критерію:

Т_сп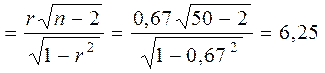

За таблицею критичних точок розподілу Стьюдента (Додаток Ж) знайдемо критичне значення критерію при рівні значимості a= 0,05 і числі степенів вільності k = n – 2 = 50 – 2 = 48: t_кр = t_кр (0,05; 48) = 2,01. Порівнюючи, одержимо, що Т_сп > t_кр .Отже, нульову гіпотезу варто відкинути. Це значить, що коефіцієнт кореляції значимо відрізняється від нуля й ознаки Х и У корельовані. Таким чином, приймаємо гіпотезу про лінійну кореляційну залежність між ознаками Х и У.

Завдання 10. Виходячи з виду кореляційного поля й емпіричної ламаної регресії, припустимо, що ознаки Х и У зв'язані параболічною залежністю . Для визначення коефіцієнтів a, b, с заповнимо таблицю, використовуючи пакет програм Excel.

Для стислості записів розрахункову таблицю приводимо не цілком, а тільки початкову та кінцеву її частини.

i	X	Y	X^2	X^3	X^4	XY	X^2Y
1	1.13	8.4	1.2769	1.443	1.6305	9.492	10.73
2	1.14	7.1	1.2996	1.482	1.689	8.094	9.227
3	1.13	7.7	1.2769	1.443	1.6305	8.701	9.832
4	1.13	7.6	1.2769	1.443	1.6305	8.588	9.704
5	1.14	8.2	1.2996	1.482	1.689	9.348	10.66
6	1.09	6.9	1.1881	1.295	1.4116	7.521	8.198
7	1.53	10.9	2.3409	3.582	5.4798	16.68	25.52
8	1.5	11.4	2.25	3.375	5.0625	17.1	25.65
9	1.44	13.5	2.0736	2.986	4.2998	19.44	27.99
10	1.39	9.5	1.9321	2.686	3.733	13.21	18.35
11	1.5	9.2	2.25	3.375	5.0625	13.8	20.7
…	…	…	…	…	…	…	…
49	1.15	9.8	1.3225	1.521	1.749	11.27	12.96
50	1.29	6.1	1.6641	2.147	2.7692	7.869	10.15
Сума	57.49	361.9	67.4615	80.785	98.6948	428.634	518.2944

Використовуючи формулу (5.13) пункту 5.7, складемо лінійну систему:

50a +          57.49b +     67.4615c     =       361.9

57.49a +     67.4615b +  80.7851c     =       428.634

67.4615a +  80.7851 b+  98.6948c     =       518.2944

Розв’яжемо систему за правилом Крамера. Обчислимо головний і допоміжні визначники системи:

	50	57.49	67.4615
D =	57.49	67.4615	80.7851	= 3.8868
	67.4615	80.7851	98.6948
	361.9	57.49	67.4615
D1 =	428.634	67.4615	80.7851	= 21.5367
	518.2944	80.7851	98.6948
	50	361.9	67.4615
D2 =	57.49	428.634	80.7851	= -23.8198
	67.4615	518.2944	98.6948
	50	57.49	361.9
D3 =	57.49	67.4615	428.634	= 25.1881
	67.4615	80.7851	518.2944

Запишемо рішення системи за формулами Крамера:

a = D1/D=5,541; b = D2/D= –1,128;  c = D3/D=6,48.

Отже, рівняння нелінійної параболічної регресії має вид :

 = 5,541 –6,128х +6,48х².

Завдання 11. Побудуємо отримані лінії регресії в одній системі координат (рис. 5.4).

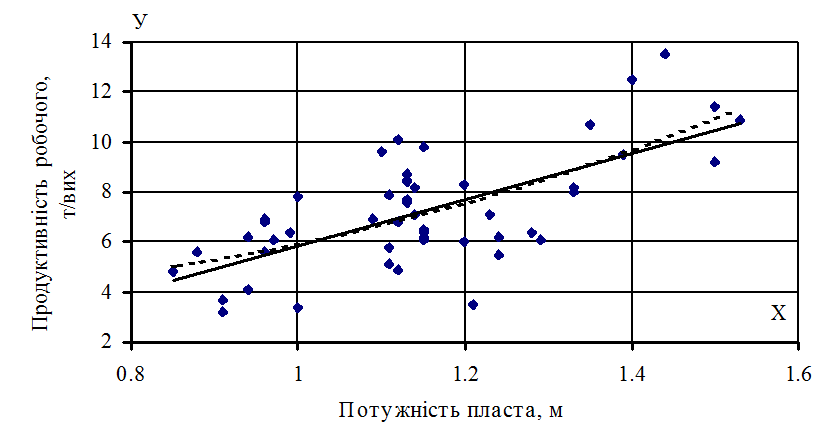
Рисунок 5.4

Тут суцільна лінія зображає лінійну регресію, а пунктирна лінія – параболічну регресію.

Завдання 12. Для всіх моделей розрахуємо теоретичний коефіцієнт детермінації і теоретичне кореляційне відношення; середню квадратичну похибку рівняння; середню відносну похибку апроксимації.

Використовуючи рівняння лінійної регресії  = 9,21×х – 3,36
і параболічної регресії  = 5,541 –6,128х +6,48х², обчислимо теоретичні значення ознаки У. Заповнимо таблиці.

Для стислості записів розрахункові таблиці приводимо не цілком.

а)   спочатку зробимо розрахунки усіх показників для лінійної регресії

 = 9,21×х – 3,36 .

i	xi	уi	yiтеор	δi=yiтеор – yi	δi2	÷δi / yi÷
1	1.13	8.4	7.0473	-1.3527	1.8298	0.1610	0.0364
2	1.14	7.1	7.1394	0.0394	0.0016	0.0055	0.0097
3	1.13	7.7	7.0473	-0.6527	0.4260	0.0848	0.0364
…	…	…	…	…	…	…	…
49	1.15	9.8	7.2315	-2.5685	6.5972	0.2621	0.0000
50	1.29	6.1	8.5209	2.4209	5.8608	0.3969	1.6458
Сума					139.096	10.8476	115.3217