Математична статистика в гірничо-геологічних розрахунках, страница 35

Після заповнення 8-го стовпця відзначаємо, що два останніх елементи в цьому стовпці менше п'яти. Оскільки в критерії Пірсона потрібно, щоб у кожнім інтервалі було не менше п'яти одиниць, то об'єднаємо частоти трьох останніх інтервалів N_i^* – для 8-го стовпця;  N_i – для 3-го стовпці.

11-ий стовпець заповнюємо за формулою:

В_i =.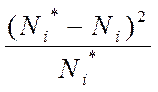

12-ий стовпець – контрольний. Він обчислюється за формулою:

V_i =.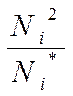

Зробимо перевірку: 49 + 7,4065 = 56,4065.    Вірно.

Запишемо спостережуване значення критерію c² _сп = 7,4065.

Виберемо рівень значимості помилки  a=0,01.

Число степенів вільності дорівнює k=l –3, де l – число інтервалів після об'єднання. У нашому випадку число інтервалів після об'єднання
l=5. Тоді число степенів вільності дорівнює k=5 –3 = 2. По таблиці критичних крапок c² (Додаток Е) знаходимо c²_кр(0,05; 2)=6,0.

Порівнюємо:        c²_набл > c²_кр.

Отже, необхідно відкинути гіпотезу про нормальний закон розподілу ознаки Х.

5. 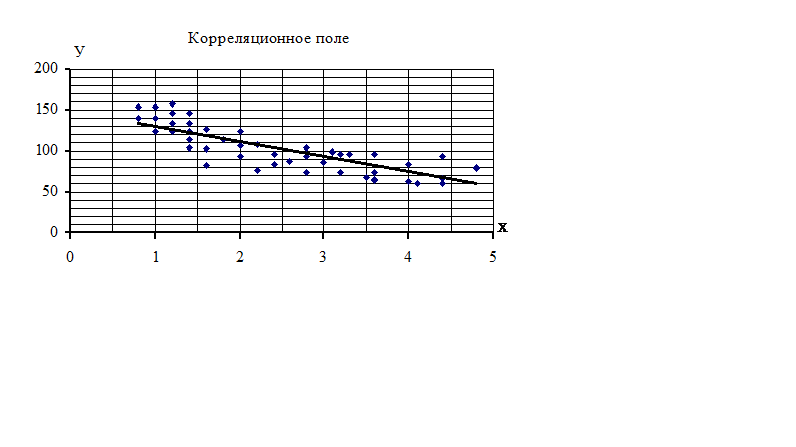 Для ознак X і Y побудуємо кореляційне поле в системі координат ХОУ, використовуючи вихідну таблицю.

Рисунок 9.6

Кореляційне поле на даному малюнку характеризується набором з 49 точок, причому можна помітити, що зі збільшенням  варіант ознаки Х  фактор У в середньому убуває. Аналіз отриманого поля розсіювання дозволяє припускати наявність  від’ємної лінійної кореляційної залежності між ознаками Х и У.

6.   Рівняння лінійної регресії має вид: у = кх + b, де параметри к и b визначаються по методу найменших квадратів з умови мінімального відхилення вихідних точок кореляційного поля від прямої регресії. Параметри к и b обчислюються по формулах (дивись розрахункові формули (5.5-5.6) із пункту 5.4:

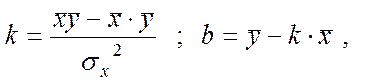
          де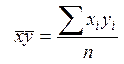      

Для розрахунку необхідних величин заповнимо таблицю. Її заповнення й обчислення рекомендуємо виконувати в Excel. Для стислості записів розрахункову таблицю приводимо не цілком, а тільки початкову та кінцеву її частини

i	X	Y	х2	у2	Х×У
1	0,8	140	0,64	19600	112
2	0,8	154	0,64	23716	123,2
3	1	124	1	15376	124
4	1	140	1	19600	140
5	1	154	1	23716	154
6	1,2	124	1,44	15376	148,8
. . .	. . .	. . .	. . .	. . .	. . .
47	4,4	60	19,36	3600	264
48	4,4	94	19,36	8836	413,6
49	4,8	79	23,04	6241	379,2
Сума	126,2	4949	396,64	536679	11425,7

Звідси одержимо:

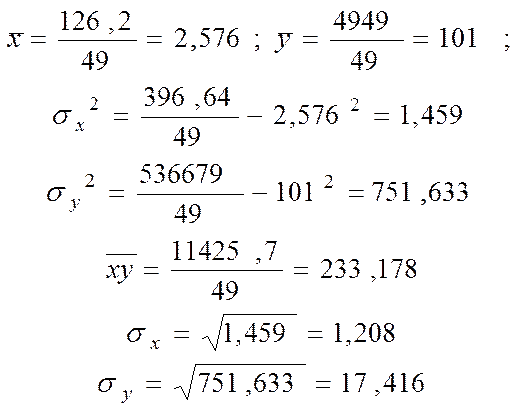
Отже, параметри рівняння регресії рівні:

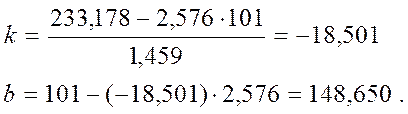
Остаточно, рівняння лінійної регресії має вигляд :

у = –18,501×х + 148,65  .

Визначимо вибірковий коефіцієнт кореляції за формулою

r = k×S_x / S_y.

Одержимо r = – 0,815.

Перевіримо коефіцієнт кореляції на значимість.

Основна гіпотеза            H ₀ :, r_г = 0

Конкуруюча гіпотеза     H ₁ : r_г ¹ 0.

Для перевірки гіпотези H ₀  обчислимо спостережуване значення:

Т_сп 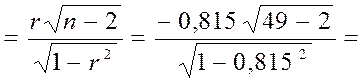 – 9,64

За таблицею критичних точок розподілу Стьюдента знаходимо критичне значення критерію при рівні значущості помилки a = 0,05 і числі степенів вільності

k = n – 2 = 49 – 2 = 47. Маємо  t_кр = t_кр (0,05; 47) = 2,01.

Порівнюючи, одержимо, що ïТ_набл ï> t_кр .

Отже, нульову гіпотезу варто відкинути. Це значить, що коефіцієнт кореляції значимий відрізняється від нуля, і ознаки Х и У корельовані.

Знайдемо коефіцієнт детермінації, що для випадку лінійної регресії дорівнює квадрату коефіцієнта кореляції: R = r²  . Одержимо:

R² = (–0,815)² = 0,66. Він говорить про те, що 66% варіації величини опускання покрівлі пояснюється варіацією швидкості посування очисного вибою. Для визначення сили зв'язку між ознаками використовуємо шкалу Чедока.

Для нашого випадку R² = 0,66. Тому на підставі шкали Чедока (див. пункт 5.6) робимо висновок про те, що між величиною опускання покрівлі і швидкістю посування очисного вибою існує помітний зв'язок.

8.   По рівнянню регресії –18,501×х + 148,65    побудуємо пряму в тій самій системі координат, що й кореляційне поле. З цією метою розрахуємо координати двох точок:

х₁ = 1 ;    у₁=  –18,501×1 + 148,65  = 130,2

х₂  = 4 ,   у₂ =  –18,501×4 + 148,65  = 74,7

Побудуємо точки на графіку і з'єднаємо їх прямою (Рис. 9.6). Одержимо лінію регресії.

9.  Обчислимо погрішності рівняння регресії.

а)   абсолютна погрішність рівняння дорівнює:

S_рівн  =  15,879

б)   відносна погрішність  рівняння дорівнює:

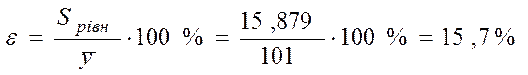
Звідси видно, що відносна помилка обчислень по отриманому рівнянню регресії складає 15,7%. 

10.  Використовуємо отримане рівняння регресії для точкового прогнозу показника У при X = 1,5 м/добу.

у_{прогноз} = –18,501×1,5 + 148,65 = 120,91 мм.

Отже, при швидкості посування очисного вибою 1,5 м/добу величина опускання покрівлі прогнозується рівної 120,91 мм. Помилка прогнозу складає не більш 15,7%.