Математична статистика в гірничо-геологічних розрахунках, страница 4

Х	1,13	1,14	1,13	1,13	1,14	1,09	1,53	1,5	1,44	1,4	1,5	1,35	1,4
У	8,4	7,1	7,7	7,6	8,2	6,9	10,9	11,4	13,5	9,5	9,2	10,7	12,5
Х	1,11	0,91	0,96	0,96	0,96	1,23	0,97	1,11	0,99	1	1,33	1,15	1,15
У	7,9	3,7	5,6	6,8	6,9	7,1	6,1	5,8	6,4	3,4	8,2	6,5	6,2
Х	1,12	1,15	1,15	0,88	1,28	1,12	1,2	1,24	0,85	1,2	1,12	1,24	0,91
У	4,9	6,4	6,1	5,6	6,4	6,8	6	5,5	4,8	3,5	10,1	6,2	3,2
Х	1	0,94	1,11	1,13	1,13	1,33	0,94	0,83	1,1	1,5	1,2	1,15	1,29
У	7,8	4,1	5,1	8,5	8,7	8	6,2	14	9,6	1	8,3	9,8	6,1

1. Провести первинну обробку статистичних даних, включаючи перевірку даних. Результати представити у виді таблиць. Побудувати статистичні ряди для кожної ознаки.

2. Побудувати гістограму, полігон відносних частот і кумуляту по кожній ознаці.

3. Використовуючи метод “умовного нуля”, визначити числові характеристики вибірок по кожній ознаці: вибіркове середнє; вибіркову дисперсію; виправлену вибіркову дисперсію; виправлене вибіркове середнє квадратичне відхилення. Дати пояснення отриманим результатам.

4. Для кожної ознаки побудувати 99% чи 95% довірчі інтервали для оцінки генеральних середніх, генеральних середніх квадратичних відхилень. Дати пояснення отриманим результатам.

5. При рівні значущості ( a=0,05 чи a=0,1 ) перевірити гіпотези про нормальні закони розподілу генеральних сукупностей по кожній ознаці.

6. Для ознак X і Y побудувати кореляційне поле, емпіричну ламану регресії і дати попередній аналіз залежності між ознаками.

7. Для ознак X і Y обчислити емпіричний коефіцієнт детермінації й емпіричне кореляційне відношення.

8. Визначити параметри рівняння лінійної регресії.

9. Визначити коефіцієнт кореляції і перевірити його на значущість. Зробити висновок про наявність лінійного зв'язку між ознаками.

10. Скласти нелінійне рівняння регресії, вибравши відповідний тип нелінійності.

11. Побудувати отримані лінії регресії в одній системі координат.

12. Для всіх моделей розрахувати теоретичний коефіцієнт детермінації і теоретичне кореляційне відношення; середню квадратичну похибка рівняння; середню відносну похибка апроксимації.

13. Використовуючи краще з отриманих рівнянь регресії дати точковий прогноз значення У при потужності пласта X = 1,8м .

Рішення задачі почнемо з перевірки вихідних даних. Побудуємо кореляційне поле (рис. 1.3), у якому представлені 52 точки (обсяг вибірки n = 52).

 

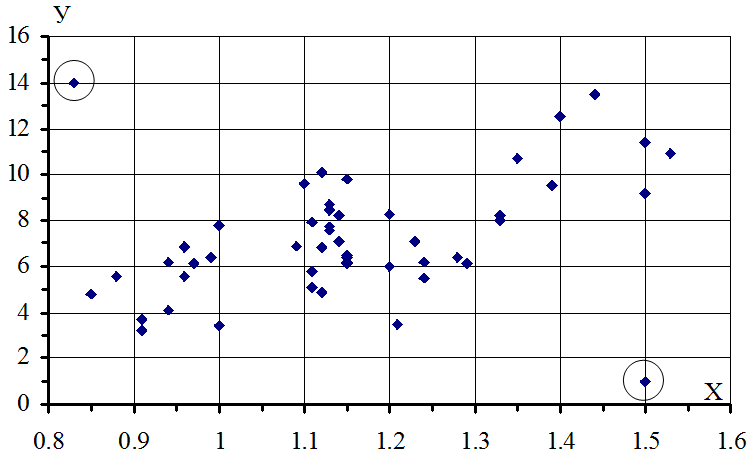Рисунок 1.3

З побудованої діаграми бачимо, що дві точки (0,83; 14) і (1,5; 1) “вискакують” із загальної сукупності. Аналіз вихідних даних з позиції можливості більшої продуктивності (у=14 т/вих) при малій потужності пласта (х = 0,83 м) і малої продуктивності (у=1 т/вих) при великій потужності пласта (х=1,5 м) дозволяє віднести ці точки до помилкових і виключити їх з подальшого розгляду. Отже, обсяг вибірки на цьому етапі приймається n = 50.

Продовжимо рішення задачі і зробимо первинну обробку даних..

а) Для ознаки Х визначимо найбільше і найменше значення ознаки:

X_min=0,85 ;  X_max=1,53 .

Число інтервалів розбивки визначимо за формулою Стерджеса:

k =1 + 3,322× lg n = 1 + 3,322× lg 50 = 6,6 » 7.

Знайдемо крок розбивки за формулою h = (Х_max – X_min) / k.

У даному випадку h = (1,53 – 0,85) / 7 = 0,097. Приймемо h = 0,1.

Зробимо групування даних для ознаки Х. Для цього підрахуємо, скільки значень ознаки Х потрапить у кожний з інтервалів розбивки. Причому, при збігу значення ознаки з однієї з границь інтервалу, включаємо це значення в лівий інтервал. Результати групування
заносимо в табл. 1.2. У третьому стовпці таблиці заносяться штрихові відмітки. Це зручний прийом підрахунку частот. Починають з першого елемента вибірки. У нашому випадку він дорівнює 1,13. Потім знаходять інтервал (1,05 – 1,15), у який це спостереження попадає, і ставлять у третьому стовпці штрихову відмітку I. Інші спостереження обробляють аналогічно, у тому порядку, у якому вони представлені в початковій
вибірці.

Якщо дослідник може використовувати табличний процесор Excel, то після введення ознаки Х можна дані розсортувати в порядку зростання, і тоді штрихові відмітки не знадобляться. Треба тільки розділити отриманий відсортований ряд на визначені інтервали і підрахувати число варіант, що попали в кожний інтервал розбивки.

б) Для ознаки У визначимо найбільше і найменше значення ознаки:

У_min=3,2 ;    У_мах=13,5 .

Визначимо число інтервалів:

k =1 + 3,322× lg n = 1 + 3,322× lg 50 = 7

Знайдемо крок розбивки h = (13,5 – 3,2) / 7 = 1,471. Приймемо h=1,48.

Зробимо групування даних для ознаки У. Результати групування заносимо в таблицю 1.3.

За результатами таблиць записуємо статистичні ряди:

для ознаки Х – таблиця. 1.4;

для ознаки У – таблиця. 1.5.

Таблиця 1.2 – Обробка ознаки Х