Математична статистика в гірничо-геологічних розрахунках, страница 15

4)   Перевірка моделі на адекватність за критерієм Фішера при рівні значущості a = 0,05 підтверджує адекватність моделі, тому що спостережуване значення критерію F=13,389 більше критичного значення Fкр = 3,592.

5.9    Оцінка похибки моделі

Порівняння різних моделей здійснюється за такими показниками:

·  За коефіцієнтами детермінації (теоретичними) і порівняння їх з емпіричним коефіцієнтом детермінації. Чим більше коефіцієнт R²_теор і чим ближче він до R²_эмпір, тим представлене рівняння регресії краще

описує залежність між ознаками Х и У.

·  За середньою відносною похибкою апроксимації:

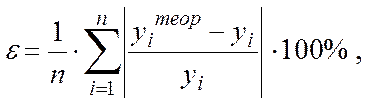                       (5.15)

де       y_i^теор – індивідуальні значення результативної ознаки У, розраховані по рівнянню регресії;

y_i^теор=f(x_i); у_i – значення ознаки У з вибірки.

Чим менше середня відносна похибка апроксимації, тим модель краще описує залежність між ознаками. Для якісної оцінки моделі по відносній похибці апроксимації використовують наступну шкалу:

e	< 10%	10 –20%	20– 50%	>50%
Висновок	Висока точність прогнозу	Гарна точність прогнозу	Задовільна точність прогнозу	Незадовільна точність прогнозу

·  За середньою квадратичною похибкою рівняння:

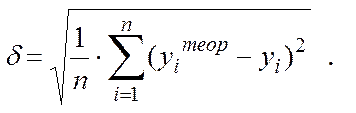                          (5.16)

Для розрахунку перелічених характеристик потрібно після того, як було отримане рівняння регресії (лінійне чи нелінійне), заповнити наступну таблицю:

i	xi	уi	yiтеор	δi=yiтеор – yi	δi2	÷δi / yi÷
1
2
. . .
n
Сума					S	S	S

Далі, маючи значення сум цієї таблиці, виконують розрахунки за формулами (14-15). Останній стовпець дуже зручно використовувати для обчислювання коефіцієнта детермінації.

5.10  Задача 1. Установлення кореляційної залежності

Продовжимо рішення задачі 1. Виконаємо завдання 6 цієї задачі.

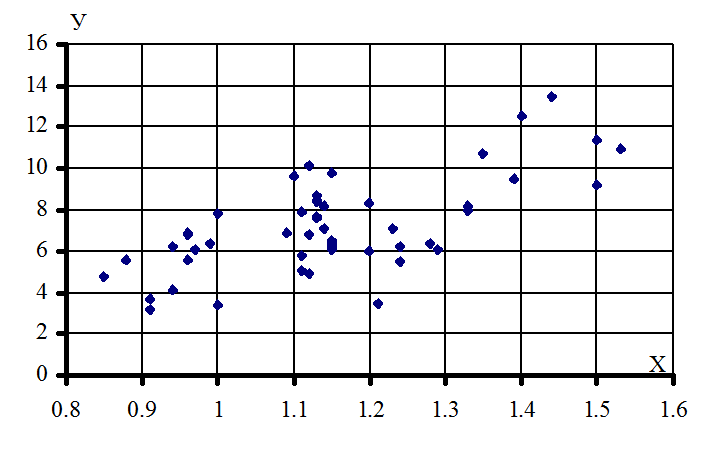Кореляційне поле має вид:

Рисунок 5.2

Для побудови емпіричної ламаної регресії зробимо розрахунок точок ,

де       х_j – середини інтервалів розбивки ознаки Х;

– середні групові значення ознаки У в кожнім інтервалі ознаки Х: 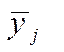= (Σ y_i)/n_j .

Інтервали по ознаці Х візьмемо з п. 2.4. Заповнимо таблицю.

Інтервал по Х	0,85-0,95	0,95-1,05	1,05-1,15	1,15-1,25	1,25-1,35	1,35-1,45	1,45-1,55
х j	0,9	1	1,1	1,2	1,3	1,4	1,5
nj	6	7	20	6	5	3	3
у i	4,8 5,6 3,2 3,7 4,1 6,2	5,6  6,8 6,9  6,1 6,4  3,4 7,8	6,9 9,6 5,1 5,8 7,9 4,9 6,8 10,1 7,6 7,7 8,4 8,5 8,7 7,1 8,2 6,1 6,2 6,4 6,5 9,8	6  8,3 3,5 7,1 5,5 6,2	6,4  6,1 8  8,2 10,7	9,5  12,5 13,5	9,2 11,4 10,9
	4,6	6,14	7,42	6,1	7,88	11,83	10,5

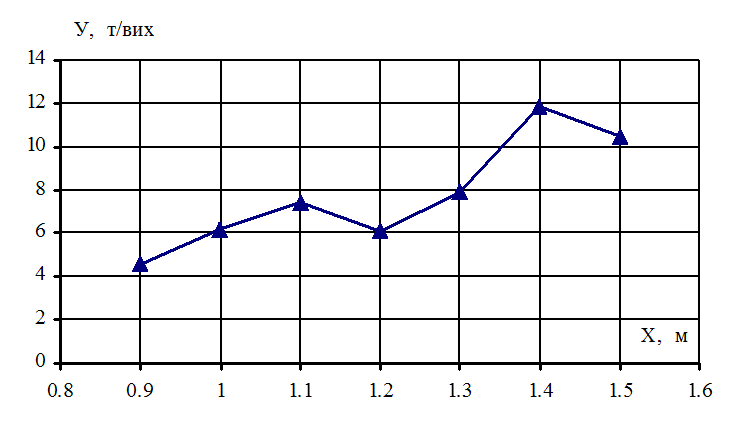Побудуємо емпіричну ламану по точках .

Рисунок 5.3

Аналіз кореляційного поля й емпіричної ламаній дозволяє припустити наявність прямої додатної кореляційної залежності між ознаками Х и У.

Виконаємо завдання 7 задачі 1. Для розрахунку емпіричного коефіцієнта детермінації й емпіричного кореляційного відношення використовуємо дані (розраховані в п. 2.4) і 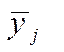– середні групові значення ознаки У.

Знайдемо міжгрупову дисперсію результативної ознаки У

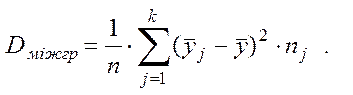
D_міжгр = ((4,6–7,285)² + (6,14–7,285)² + (7,42–7,285)² +

+ (6,1–7,285)²+(7,88–7,285)²+(11,83–7,285)²+(10,5–7,285)²⁾ =3,119

Емпіричний коефіцієнт детермінації дорівнює:

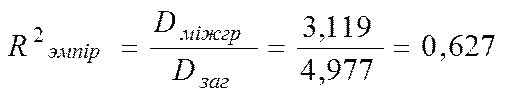
Отже, 62,7% варіації середньої за місяць продуктивності робітника порозумівається варіацією потужності пласта.

Емпіричне кореляційне відношення дорівнює     Воно вказує на значний кореляційний зв'язок між ознаками Х и У.

Розв’яжемо завдання 8. Визначимо параметри рівняння лінійної регресії по формулах (5.5–5.6), пункт 5.4.

З цією метою, використовуючи вихідні дані, створимо таблицю. Її заповнення й обчислення рекомендуємо виконувати в Excel. Для стислості записів розрахункову таблицю приводимо не цілком, а тільки початкову та кінцеву її частини.

i	X	Y	X^2	Y^2	XY
1	1.13	8.4	1.2769	70.56	9.492
2	1.14	7.1	1.2996	50.41	8.094
3	1.13	7.7	1.2769	59.29	8.701
4	1.13	7.6	1.2769	57.76	8.588
5	1.14	8.2	1.2996	67.24	9.348
6	1.09	6.9	1.1881	47.61	7.521
7	1.53	10.9	2.3409	118.81	16.68
8	1.5	11.4	2.25	129.96	17.1
9	1.44	13.5	2.0736	182.25	19.44
10	1.39	9.5	1.9321	90.25	13.21
11	1.5	9.2	2.25	84.64	13.8
12	1.35	10.7	1.8225	114.49	14.45
13	1.4	12.5	1.96	156.25	17.5
14	1.11	7.9	1.2321	62.41	8.769
15	0.91	3.7	0.8281	13.69	3.367
16	0.96	5.6	0.9216	31.36	5.376
...	...	...	...	...	...
47	1.2	8.3	1.44	68.89	9.96
48	1.1	9.6	1.21	92.16	10.56
49	1.15	9.8	1.3225	96.04	11.27
50	1.29	6.1	1.6641	37.21	7.869
Сума	57.49	361.9	67.462	2873.9	428.6
Середнє	1.1498	7.238	1.3492	57.477	8.5727