Математична статистика в гірничо-геологічних розрахунках, страница 3

Дуже важливо, аби дані, отримані при статистичному аналізі, були ретельно перевірені і відредаговані до початку більш складного аналізу. Ніколи не слід забувати прислів'я статистиків: «Сміття на вході – сміття на виході».

Перевірка даних може здійснюватися на багатьох етапах статистичних досліджень:

·  за кореляційним полем до первинної обробки даних при двовимірному статистичному аналізі;

·  за статистичним рядом при одномірному аналізі;

·  за законом розподілу при одномірному аналізі.

Для перевірки за кореляційним полем випадкових величин Х и У, не розбитих на дискретні категорії, необхідно побудувати точки в прямокутній системі координат (х₁ ;y₁), (х₂ ;y₂), ..., (х_i ;y_i), …, (х_n ;y_n) . Отримане поле точок (діаграма розсіювання) дозволяє визначити грубі помилки і викиди, не помічені одномірним аналізом кожної з перемінних.

Для приклада наведемо кореляційне поле (рис. 1.1), де відзначені дві точки, які явно є помилковими.

У випадках виявлення подібних точок не слід автоматично виключати їх з вибірки. Спочатку треба проаналізувати ситуацію, виявити можливі шляхи помилок у кожнім конкретному випадку, а потім приймати рішення по виключенню даних з вибірки. Якщо таких точок буде багато, то, можливо, їх треба виділити в окрему групу.

У деяких випадках за допомогою кореляційного поля можна виявити не тільки аномальності в числових даних, але й установити деякі закономірності.

 

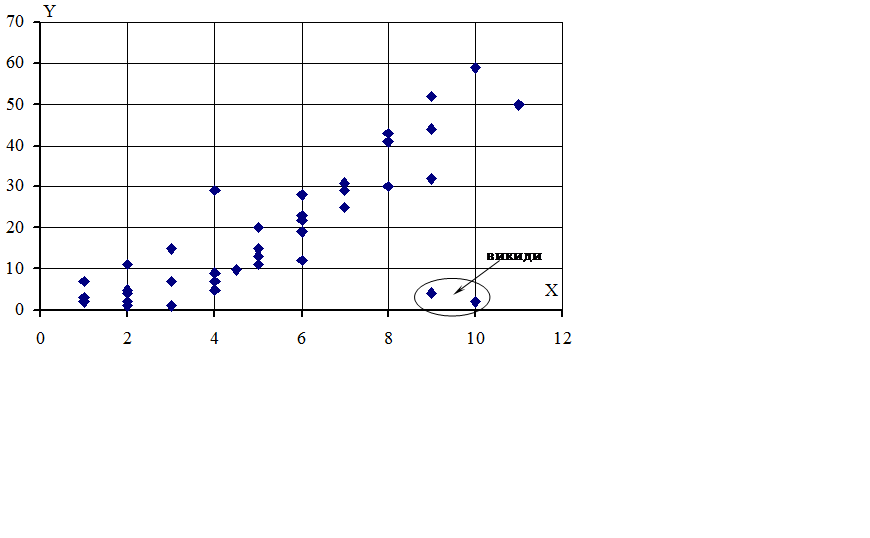Рисунок 1.1

Візьмемо такий приклад. Припустимо, потрібно установити, як потужність розроблювального пласта впливає на добовий дільничний видобуток вугілля. Була узята проста випадкова безповторна вибірка по ряду показників з декількох шахт. Побудовано кореляційне поле (рис. 1.2).

 

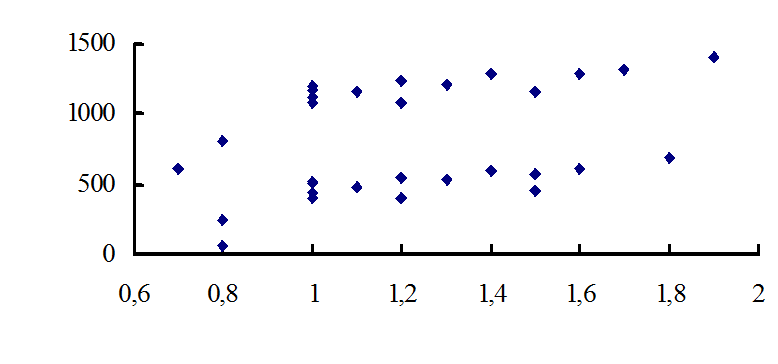
Рисунок 1.2

З даної діаграми видно, що множина точок кореляційного поля чітко розпадається на дві підмножини (верхня В та нижня Н). Наступний аналіз даних з обліком інших, у тому числі і якісних, ознак, виявив, що підмножина Н відповідає викидонебезпечним пластам вугілля, а підмножина В – невикидонебезпечним пластам. Тому на даному етапі дослідження доцільно проводити обробку статистичних даних окремо для викидонебезпечних і невикидонебезпечних пластів.

1.2  Групування статистичних даних

Первинна обробка статистичних даних дозволяє одержати з вихідного матеріалу шляхом групування статистичний ряд (точковий чи інтервальний), а також емпіричну щільність розподілу й емпіричну функцію розподілу ознаки Х. Основні етапи первинної обробки:

а)   визначення мінімального (х_min) і максимального (х_mах) елементів вибірки;

б)   визначення раціонального числа інтервалів розбивки. Тут потрібно використовувати формулу Стерджеса:

k = 1 + 3,322× lg n           при n £ 100;

k £ 5× lg n                         при n > 100.

в)   визначення кроку інтервалу h = (х_max – х_min) / k

*допускається округляти в зручну для користувача сторону.

д)   підрахунок числа частот n_i (можна за допомогою штрихової відмітки);

е)   заповнення таблиці.

Шаблон таблиці наводиться нижче.

№	Інтервали	Штрихова відмітка	Частота ni	Середина інтервалу хi	Частості wi	Ордината гістограми	Накопичені частоти	Ордината кумуляти
1
2
…
S			S1		S2	S3

Частості обчислюються за формулою: w_i= n_i/n.

Гістограма характеризує емпіричну щільність розподілу, і ординати її точок визначаються за формулою: y_i= w_i/h. Також по цих точках будують полігон відносних частот. Якщо щільність розподілу генеральної сукупності є досить гладкою функцією, то полігон відносних частот є ліпшим наближенням щільності, ніж гістограма.

Накопичені частоти для кожного i -го інтервалу знаходяться як суми частот n_i , починаючи з першого інтервалу по i -ий.

Кумулята є графіком емпіричної функції розподілу і її ординати дорівнюють накопиченим частотам, поділеним на обсяг вибірки n.

Останній рядок таблиці S містить суми елементів деяких стовпців і використовується для контролю. При правильному заповненні таблиці повинні виконуватися наступні рівності:

S1 = n ; S2 = 1 ; S3×h =1 .

Заповнена таблиця дозволяє записати статистичний ряд (точковий або інтервальний), а також побудувати гістограму, кумуляту і полігон для даного розподілу.

1.3  Графічне представлення статистичних даних

Графічно статистичні дані представляються гістограмою і полігоном відносних частот, а також кумулятою. При побудові гістограми на осі абсцис відкладають інтервали розбивки ознаки Х, при побудові полігона – середини інтервалів х _i . По осі ординат у кожнім випадку відкладають ординати w_i/h. Отриману східчасту фігуру називають гістограмою, ламану лінію – полігоном.

При побудові кумуляти на осі абсцис відкладають інтервали розбивки ознаки Х, а по осі ординат відкладають розраховані ординати кумуляти, причому крайня ліва точка має нульову ординату, інші значення ординат беруться з таблиці і відповідають межам інтервалів.

1.4  Задача 1. Первинна обробка

Як приклад візьмемо задачу про встановлення кореляційної залежності між потужністю пласта і продуктивністю робітника. Надалі ця задача буде використовуватися нами як основна навчальна на всіх етапах дослідження.

Задача1. У нижченаведеній таблиці зібрані дані за продуктивність праці робочого очисного вибою для стругових установок на антрацитових шахтах. Позначення: Х – потужність пласта, м; У – продуктивність робітника (середня за місяць), т/вихід.

Таблиця 1.1