Математична статистика в гірничо-геологічних розрахунках, страница 5

№	Інтервали	Штрихова відмітка	Частоти ni	Середина інтервалу хi	Частості	Ордината гістограми	Накопичені частоти	Ордината кумуляти
1	0,85 - 0,95	IIIIII	6	0,9	0,12	1,2	6	0,12
2	0,95 -1,05	IIIIIII	7	1	0,14	1,4	13	0,26
3	1,05 -1,15	IIIIIIIIIIIIIIIIIIII	20	1,1	0,4	4	33	0,66
4	1,15 -1,25	IIIIII	6	1,2	0,12	1,2	39	0,78
5	1,25 -1,35	IIIII	5	1,3	0,1	1	44	0,88
6	1,35 -1,45	III	3	1,4	0,06	0,6	47	0,94
7	1,45 -1,55	III	3	1,5	0,06	0,6	50	1
S			50		1	10

Таблиця 1.3 – Обробка ознаки В

№	Інтервали	Штрихова відмітка	Частоти ni	Середина інтервалу yi	Частості	Ордината гістограми	Накопичені частоти	Ордината кумуляти
1	3,2 - 4,68	IIIII	5	3,94	0,1	0,068	5	0,1
2	4,68 - 6,16	IIIIIIIIIIII	12	5,42	0,24	0,162	17	0,34
3	6,16 - 7,64	IIIIIIIIIIIIII	14	6,9	0,28	0,189	31	0,62
4	7,64 - 9,12	IIIIIIIIII	10	8,38	0,2	0,135	41	0,82
5	9,12 - 10,6	IIII	4	9,86	0,08	0,054	45	0,9
6	10,6 -12,08	III	3	11,34	0,06	0,041	48	0,96
7	12,08-13,56	II	2	12,82	0,04	0,027	50	1
S			50		1	0,676

Таблиця 1.4 – Ознака Х

Інтервал	0,85-0,95	0,95-1,05	1,05-1,15	1,15-1,25	1,25-1,35	1,35-1,45	1,45-1,55
х i	0,9	1	1,1	1,2	1,3	1,4	1,5
ni	6	7	20	6	5	3	3

Таблиця 1.5 – Ознака У

Інтервал	3,2- 4,68	4,68-6,16	6,16-7,64	7,64-9,12	9,12-10,6	10,6-12,08	12,08-13,56
y i	3,94	5,42	6,9	8,38	9,86	11,34	12,82
ni	5	12	14	10	4	3	2

Графічно статистичні дані представляємо гістограмою і полігоном відносних частот, а також кумулятою. При побудові гістограми на осі абсцис відкладають інтервали розбивки ознаки Х, при побудові полігона – середини інтервалів розбивки ознаки х _i . По осі ординат у кожнім випадку відкладають ординати w_i/h. Отриману східчасту фігуру називають гістограмою, ламану лінію – полігоном.

 

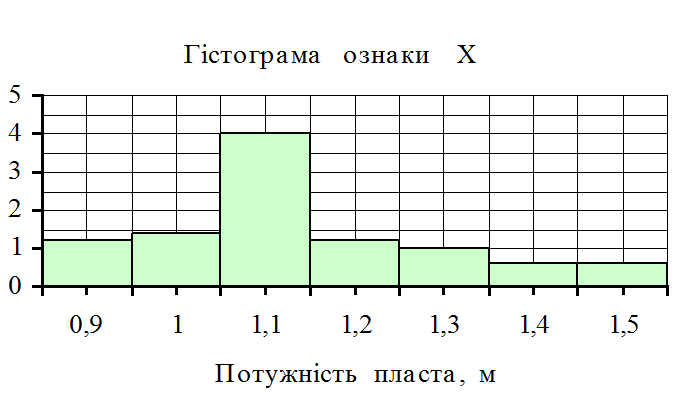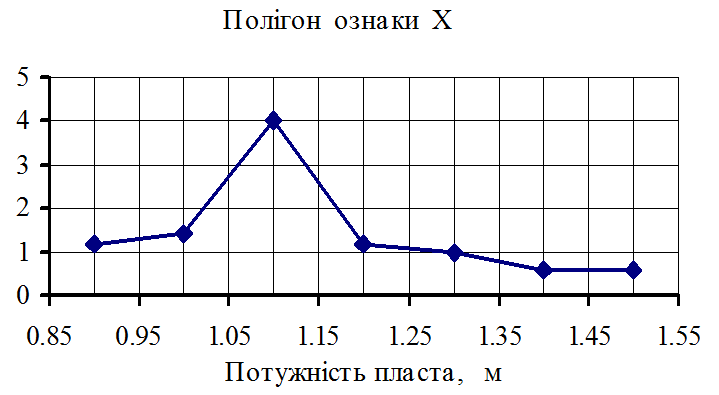Рисунок 1.3

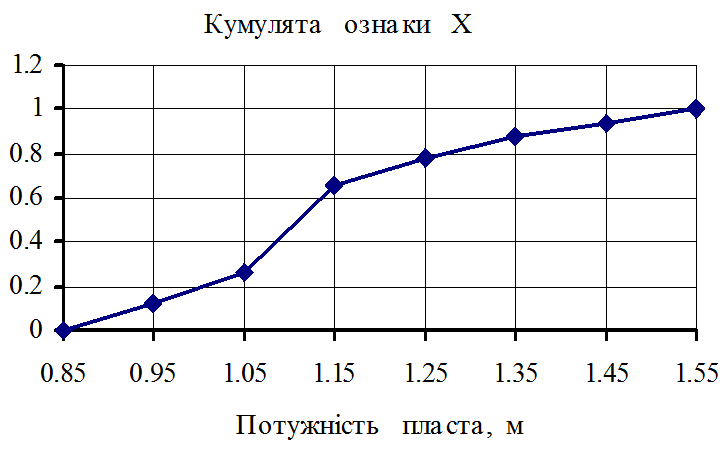Рисунок 1.4

Рисунок 1.5

 

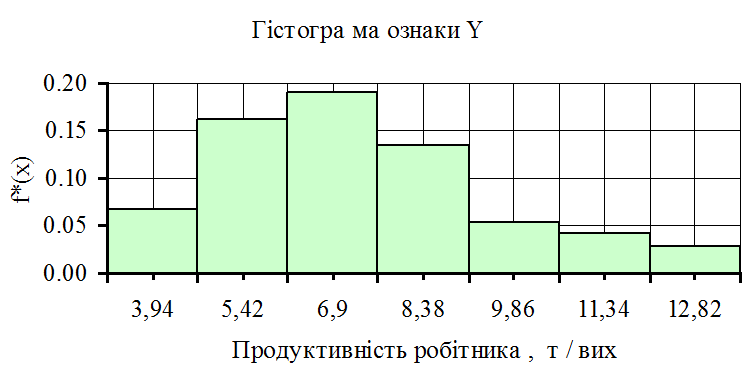
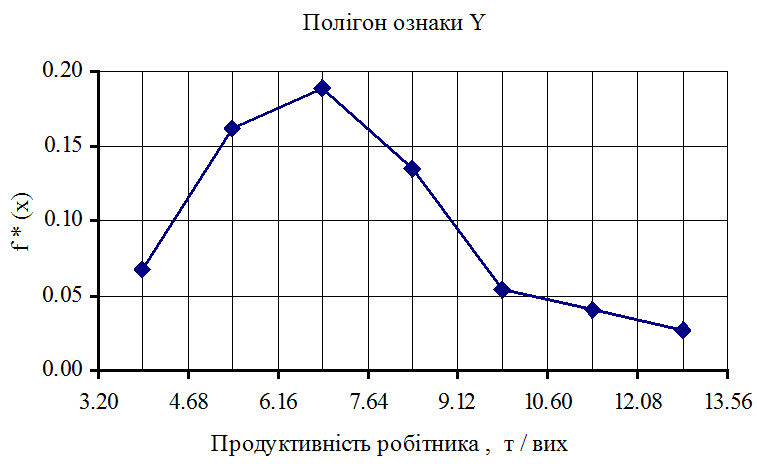Рисунок 1.6

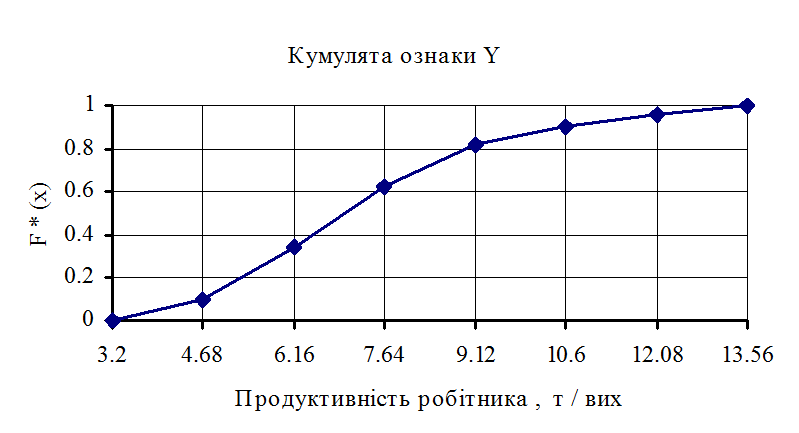
Рисунок 1.7

Рисунок 1.8

2. Точкові оцінки параметрів розподілу

Точкова оцінка деякого параметра розподілу визначається за даними вибірки, записується одним числом і служить оцінкою параметра розподілу генеральної сукупності. Така оцінка називається вибірковою.

Приведемо основні точкові оцінки параметрів розподілу.

Математичне сподівання випадкової величини оцінюється по вибірковій середній  ; дисперсія – по вибірковій дисперсії D_в і виправленої вибіркової дисперсії S² ; середнє квадратичне відхилення (СКВ) оцінюється по вибірковому середній квадратичному відхиленню s_в і виправленому вибірковому середньому квадратичному відхиленню S; асиметрія розподілу оцінюється по вибірковому коефіцієнту асиметрії А_s ; ексцес – по вибірковому ексцесу E_к ; мода розподілу – по вибірковій моді М_о ; медіана розподілу – по вибірковій медіані М_е . Імовірність події в моделях, що підкоряються схемі Бернуллі, оцінюється по вибірковій частці w .

Для трактування отриманих результатів розрахунку параметрів вибірки варто знати зміст кожної оцінки. Приведемо коротку їхню характеристику:

·   – характеризує середнє значення ознаки по вибірці;

·  D_в і S² – характеризують середній квадрат відхилення ознаки від середнього значення по вибірці, тільки друга характеристика є ще і незміщеною;

·  s_в і S – характеризують середнє відхилення ознаки від середнього значення по вибірці;

·   А_s – характеризує асиметрію розподілу по вибірці;

·  E_к – характеризує “крутість” (гостровершинність чи плосковершинність) розподілу по вибірці.

·  М_о – характеризує варіанту, що найчастіше зустрічається, чи значення ознаки, якому відповідає точка максимуму щільності розподілу по вибірці;.

·  М_е – характеризує те значення ознаки, на котре приходиться середина варіаційного ряду по вибірці;

·  w – характеризує імовірність появи події А в одному іспиті.

На практиці для розрахунку перелічених величин застосовують різні формули в залежності від виду вибірки.

2.1  Незгруповані статистичні дані

Нехай вибірка значень ознаки Х являє собою незгрупований ряд чисел:

х₁ ; x₂ ; … ; х_i ; …; x_n ...

У цьому випадку розрахунок ведуть за наступними формулами:

Вибіркова середня:

 ,

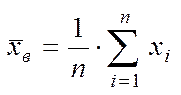Вибіркова дисперсія:

 ,

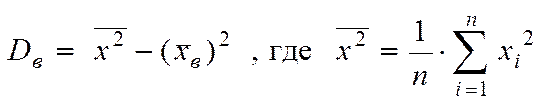Вибіркове середнє квадратичне відхилення: