Сведения из теории множеств. Операции над множествами. Теоретическая справка. Классические критерии принятия решения, страница 4

Оценочные функции могут выбираться различными. Выбор зависит как от особенностей решаемой задачи, так и от опыта и пристрастий принимающего решение. Например: .

Классические критерии принятия решения

1. Минимаксный критерий (ММ)

Этот критерий соответствует позиции крайней осторожности.

Оценочная функция

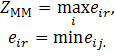
Таким образом, при выборе оптимального решения E₀ справедливо соотношение

2. Критерий Байеса-Лапласа (BL)

Пусть q_j- вероятность появления внешнего состояния F_j. Тогда

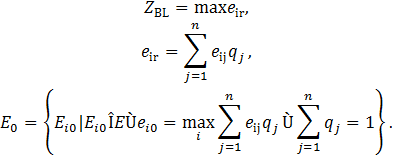
При этом полагается:

- вероятность появления состояний F_j известны и не зависят от времени;

- решение реализуется (теоретически) бесконечно много раз;

- для малого числа реализаций решения допускается некоторый риск.

Исходная позиция применяющего BL-критерий оптимистичнее, чем в случае MM-критерия, однако она предполагает более высокий уровень информированности и достаточно длинные реализации.

3. Критерий Сэвиджа (S)

Формируется оценочная функция

и строится множество оптимальных вариантов решения

Мы можем здесь интерпретировать  как потери, возникающие в состоянии F_j при замене оптимального для него варианта на вариант E_i, тогда  представляют собой - при интерпретации a_ij в качестве потерь - максимальные возможные потери в случае выбора варианта E_i, и эти потери минимизируются за счет выбора подходящего варианта E_i. По Z_s оцениваются значения результатов тех состояний, которые, вследствие выбора соответствующего распределения вероятностей, оказывают одинаковое влияние на решение.

Производные критерии

Стремление получить критерии, которые лучше приспосабливались бы к имеющейся ситуации, привело к созданию так называемых производных критериев, которые в зависимости от выбора некоторого параметра либо приводятся к классическим критериям, либо позволяют занять некоторую уравновешенную позицию.

1.Критерий Гурвица (HW)

 

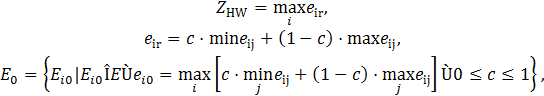
где c - весовой множитель.

Для c=1 HW-критерий превращается в MM-критерий. Для c=0 он превращается в критерий азартного игрока.

В технических системах чаще всего полагают c=0.5.

При обосновании выбора также применяют обратный порядок действий: для приглянувшегося решения вычисляют c, используемый в дальнейшем.

HW-критерий предъявляет к ситуации, в которой принимается решение, следующие требования:

- о вероятностях появления состояний F_j ничего не известно;

- с появлением состояний F_j необходимо считаться;

- реализуется лишь малое количество решений;

- допускается некоторый риск.

2. Критерий Ходжа-Лемана (HL)

Этот критерий опирается одновременно на MM-критерий и BL-критерий. С помощью параметра выражается степень доверия к используемому распределению вероятностей.

Оценочная функция

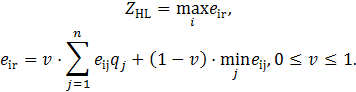
Множество оптимальных решений записывается в виде:

Выбор параметра субъективен, число реализаций не учитывается.

Для применения HL-критерия ситуация должна обладать следующими свойствами:

- вероятность появления состояний F_j неизвестны, но некоторые предположения о распределениях вероятностей возможны;

- принятое решение теоретически допускает бесконечно много реализаций;

- при малых числах реализаций допускается некоторый риск.

3. Критерий Гермейера (G)

Этот критерий ориентирован на величины потерь, т.е. на отрицательные значения всех e_ij.

Оценочная функция

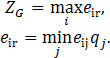
Оптимальное решение

В случае, когда встречаются e_ij>0, то переходят к строго отрицательным значениям с помощью преобразования e_ij-a (однако, следует иметь в виду, что оптимальный вариант решения будет зависеть от a).

G-критерий обобщает MM-критерий. В случае равномерного распределения q_j=1/n,j=1,...,n они становятся идентичными.

Условия применимости критерия:

- вероятности появления состояния F_j известны;

- с появлением тех или иных состояний отдельно или в комплексе необходимо считаться;

- допускается некоторый риск;

- решение может реализоваться один или много раз.

4. BL(MM)-критерий (составной критерий)

Прежде всего по MM-критерию находят опорное значение

 

Задается из каких-либо соображений уровень допустимого риска . Определяются два множества вариантов