Степени соответствия: 1 - "соответствует", 0 - "не соответствует".
1. Описание объекта принятия решения, набор признаков, его характеризующих, диапазон четких и нечетких значений признаков.
2. Графики функций принадлежности для нечетких значений признаков.
3. Описание степеней соответствия и графики функций отображения.
4. Описание эталонных ситуаций.
5. Результаты эксперимента: описание исходных ситуаций, полученные по ним решения при конкретных степенях порогового включения.
6.Выводы по работе.
1. А.Н.Мелихов, Л.С.Бернштейн, С.Я.Коровин. Ситуационные советующие системы с нечеткой логикой. М.: Наука, 1990. - 272 с.
2. Н.Г.Малышев, Л.С.Берштейн, А.В.Боженюк. Нечеткие модели для экспертных систем в САПР. - М.: Энергоатомиздат, 1991. - 136 с.
3. В.В.Моторин, А.А.Кочетыгов. Системы и методы искусственного интеллекта: Учебное пособие. Тула: ТулГУ, 1995. - 80 с.
ЛАБОРАТОРНАЯ РАБОТА N 5
Цель работы: изучить детерминированный подход для создания систем классификации альтернатив.
Использование методов обучения для построения систем распознавания необходимо, когда отсутствует полная первоначальная информация об объекте.
Сущность процедуры обучения состоит в следующем.
Использовать необходимую априорную информацию, которая позволяет составить список объектов с указанием, к какому классу каждый из них относится.
Обозначив объекты списка как w1,..., wi, а классы - W1,..., Wm, исходную информацию можно записать в виде
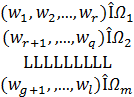
Каждый объект может быть описан на языке признаков X1,...,XN. Исходный список может быть представлен в виде обучающей последовательности
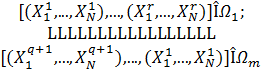
Если обучающая последовательность достаточно представительна, то есть содержит объекты, равномерно располагающиеся в областях признакового пространства соответствующих классов, то в пределе процедура обучения может сформировать такие границы классов, с помощью которых можно достичь требуемой точности работы системы распознавания.
При этом разделение должно происходить наилучшим образом.
Если ограничиться рассмотрением двух классов W1 и W2, то разделяющая классы гиперповерхность носит название дихотомии. К дихотомии можно последовательно свести и общий случай, когда m>2.
Разделяющая функция d(x)=f(x,c), где c=(c1,...,cN) представляется в виде функции скалярного произведения вектора признаков X и неизвестного вектора параметров c.
Знание разделяющей функции определяет области в N -мерном пространстве признаков; в частности, пространства и соответствуют классам W1 и W2, то есть
D1={X,f(X,c)<0};
D2={X,f(X,c)>0}.
В процессе обучения представление объектов w1,..., wi осуществляется случайным образом.
Рассмотрим простейшую схему итеративного определения вектора весов. Эта схема носит название "алгоритма перцептрона". Обозначим c(1) - начальный вектор параметров, который обычно выбирается произвольно. Тогда k-й шаг обучения выглядит следующим образом.
Если x(k)ÎW1 и cT(k)x(k)<0 то вектор c(k) заменяется на c(k+1)=c(k)+ax(k), где a - константа, постоянное корректирующее приращение.
Если x(k)ÎW2 и cT(k)x(k)>0 то c(k) заменяется на c(k+1)=c(k)-ax(k). В случае равенства c(k) не заменяется, то есть c(k+1)=c(k).
Корректирующее приращение a должно быть положительным и в данном алгоритме оно является постоянным.
Таким образом, если образ классифицирован правильно, то система подкрепляется тем, что в вектор весов c(k) не вносится никаких изменений. Если образ классифицируется неправильно и произведение cT(k)x(k) оказывается меньше нуля, когда оно должно быть больше нуля, то система наказывается увеличением значения вектора весов c(k) на величину, пропорциональную x(k). Если же произведение cT(k)x(k) оказывается большим нуля, когда оно должно быть меньше нуля, система наказывается уменьшением весов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.