Сведения из теории множеств. Операции над множествами. Теоретическая справка. Классические критерии принятия решения, страница 25

В результате действия природы появляется выборочный образ X. Классификатор должен выработать решение, определяющее класс, который, "по мнению классификатора", выбрала природа. Природа выбирает стратегии, основываясь на вероятностях P(W_i), i=1,..,N, и придерживается этих стратегий несмотря на их неоптимальность с точки зрения теории игр.

Кроме этого, классификатор может осуществлять эксперименты с тем, чтобы улучшить понимание методов, используемых природой.

Предположим, что при реализации игры между природой и классификатором, природа выбирает класс W_i и воспроизводит образ X. Тогда P(W_i/X) - вероятность принадлежности образа Х к классу W_i.

Обозначим L_ij - убытки, если классификатор принимает решение о принадлежности Х к классу W_j вместо W_i.

Так как образ Х может принадлежать любому из М классов, то средние потери определяются выражением:

                        

Это выражение  носит название условного среднего риска. Для каждого образа Х вычисляются условные средние потери  Классификатор причисляет образ Х к классу, где потери наименьшие. Классификатор, минимизирующий математическое ожидание общих потерь, называется байесовским классификатором.

Используя формулу Байеса

условный средний риск запишем в виде

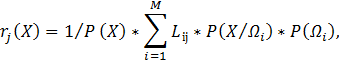
где  функция правдоподобия для класса . Общий множитель  для всех  при  сравнении  исключается. Воспользуемся частным случаем М=2. Тогда при выборе стратегии 1 средние потери

а при выборе стратегии 2

образ если . Тогда

Преобразуя это равенство с учетом того, что  получим неравенство

Это неравенство  определяет принадлежность образа Х к классу  Выражение

называется отношением правдоподобия.

Величина  называется пороговым значением :

В работе  необходимо реализовать простейшую схему разделения двоичного сигнала, состоящего из нулей и единиц, зашумленного аддитивным белым шумом.

 - гипотеза о том, что получен сигнал "0";

 - гипотеза о том, что получен сигнал "1".

Априорные вероятности  передачи  "0"  и  "1"  соответственно обозначим P(0) и P(1). Зададим матрицу потерь:

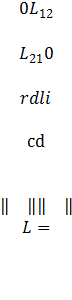
где  a₁ и a₂ - решения,  утверждающие,  что передан символ "0" или "1"; L₁₂ - потери при выборе решения a₂, когда имеем класс ; L₂₁ - потери при выборе решения a1, когда имеем класс .

Выбирается шум с нулевым средним и дисперсией . Закон распределения шума - нормальный. Тогда плотность вероятности принятого сигнала при условии передачи "0" определяется выражением:

Плотность вероятности принятого сигнала при условии передачи "1" определяется выражением:

                                                         

Отношение правдоподобия при этом принимает вид:

Система принимает решение о принадлежности к классу, если выполнены условия:

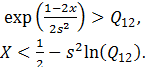
Использование байесовского  классификатора (решающего правила) требует при выводе о передаче "0" оценить условие

В частном случае при =0  приходим к интуитивному условию, что при Х<0.5 имеется значение 0.

Задание на работу

1. Сформировать псевдослучайную последовательность из 0 и 1 с заданными P(0) и P(1).

2. Добавить к сформированной последовательности нормально распределенные случайные числа с нулевым математическим ожиданием и дисперсией s².

3. Задать потери L₂₁ и L₁₂ и сформировать байесовский классификатор.

4. Путем смены s², L₂₁ и L₁₂, вероятностей P(0) и P(1) качественно оценить работу классификатора.

5. Привести исходную двоичную последовательность после работы классификатора при разных значениях параметра. Просчитать число ошибочных решений.

6. Сделать выводы по работе.

Литература

1. Дж. Ту, Р. Гонсалес. Принципы распознавания образов. - М.; Мир, 1978, -360 с.

2. А. Л. Горелик, В. А. Скрипкин. Методы распознавания. - М.; Высш. шк., 1989, -231 с.