Сведения из теории множеств. Операции над множествами. Теоретическая справка. Классические критерии принятия решения, страница 24

Сходимость алгоритма наступает при правильной классификации всех образов с помощью некоторого вектора весов. Следует отметить, что алгоритм перцептрона сходится за конечное число итераций, если заданные классы линейно разделимы.

Для классификации нескольких классов можно рассмотреть три случая разделения.

1. Каждый  из  m классов отделяется от всех остальных единственной разделяющей поверхностью. Эту задачу можно свести к задаче о разделении на два класса  и , где  - совокупность всех классов за исключением класса .

2. Каждый  класс отделим от другого класса. Задача при этом заключается в построении m(m-i)/2 решающих функций. Эти функции находятся путем применения алгоритма ко всем парам заданных классов.

3. Допускается существование m решающих функций, обладающих тем свойством, что при  для всех j¹i

Обобщенный алгоритм, основанный на третьем случае, описывается следующим образом.

Предположим, что на i-м шаге итераций процедуры обучения системе предъявляется образ x(k), принадлежащий классу . Вычисляются значения m решающих функций:         

Если выполняются условия  , то векторы весов не изменяются, то есть

Если для некоторого  то производится коррекция весов:

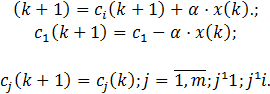
Если три класса разделимы, то предлагаемый алгоритм сходится за конечное число итераций при произвольном начальном векторе весов.

Для обучения по экономическим соображениям используется достаточно ограниченное число обучающих образов. Так для  разбиения на два класса общее число образов, предъявляемых к обучению, должно быть больше или равно удвоенной размерности векторов образов.

В общем случае число обучающих образов где R+1 - число весов, входящих в решающую функцию. Общий вид линейной решающей функции задается в виде :

где  и  - расширенные векторы.

Задание на работу

1. Получить у преподавателя значения признаков обучающих образов для двух или трех классов. Например, для

Расширенные векторы запишутся в виде

2. Выбрать начальный вектор весов. В качестве начального вектора можно взять

3. Составить  программное обеспечение по предложенному алгоритму с выдачей текущих значений коэффициентов на  каждой  итерации.

Уточнение вектора параметров с прекращается на той итерации, на которой при предъявлении всей обучающей последовательности образов значения весовых коэффициентов не изменяются.

Результатом программного обеспечения должно явиться формирование решающих функций d(x) для заданного числа классов и апробация системы распознавания на контрольных объектах.

Содержание отчета

1. Описание метода распознавания.

2. Рассчитанные выражения для решающих функций.

3. Результаты распознавания контрольных объектов.

4. Листинг программы.

5. Выводы по работе.

Литература

1. Дж. Ту, Р. Гонсалес. Принципы распознавания образов. - М.; Мир, 1989, - 360 с.

2. А. Л. Горелик, В. А. Скрипкин. Методы распознавания. - М.; Высш. шк., 1989. - 232 с.

ЛАБОРАТОРНАЯ РАБОТА N 6

ПРИНЯТИЕ РЕШЕНИЙ С ПОМОЩЬЮ ФУНКЦИИ ПРАВДОПОДОБИЯ

Цель работы: рассмотреть задачу статистической классификации как задачу принятия решений.

Теоретическая справка

Принятие решений будем рассматривать как статистическую игру, которую система классификации ведет с природой.

Игрой с нулевой суммой называется игра, в которой выигрыш одного участника точно равен по величине проигрышу другого участника. В таких играх используются байесовская стратегия, минимаксная стратегия и стратегия Неймана - Пирсона.

Задача классификации заключается в определении оптимального решения, которое обеспечивает минимизацию среднего риска или стоимости потерь. Будем трактовать стратегию, используемую условным игроком А, как состояние природы W_i. Состояния природы суть классы образов и стратегии, используемые классификатором, представляют решения, относящиеся к состояниям природы.

При каждой реализации игры выбирается стратегия W_i в соответствии с априорной вероятностью P(W_i) класса W_i.