Сведения из теории множеств. Операции над множествами. Теоретическая справка. Классические критерии принятия решения, страница 15

Теперь мы имеем два множества условных вероятностей: P(пⁱ/с_j) и P(с_j/пⁱ). Ими можно воспользоваться для установления возможного диагноза. Возникает вопрос: каким из этих двух множеств следует воспользоваться, т. е. какое из них надо построить? Было бы логичнее приступать к решению проблемы диагностирования, располагая величинами P(с_j/пⁱ). В этом случае при условии, что комплексы причин изучены, диагност мог бы сравнить комплексы следствий и выбрать среди них тот, вероятность появления которого наибольшая. Однако часто применяется P(пⁱ/с_j), а не P(с_j/пⁱ). Возражением против использования последней величины является то, что она больше, чем

Таблица 3.3. Диагностическая вероятностная таблица

первая зависит от характеристик выборки, используемой для последующей обработки. С другой стороны, P(пⁱ/с_j) практически не зависит от выборки, а определяется знаниями о причинах и следствиях.

Преимущество использования величины P(с_j/пⁱ) заключается в том, что диагност может продолжить корректирование вероятности с учетом получаемой информации. Это "корректирование" основано на хорошо известной теореме Байеса, которая может быть сформулирована следующим образом:

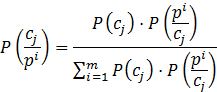
где m - число реальных комплексов следствий; P(пⁱ/с_j) - известное множество условных, или "априорных", вероятностей. Построение этого множества основано на постоянном соотношении между комплексами причин и комплексами следствий; P(с_j) - новая информация, полученная в результате исследования текущей выборки случаев; P(с_j/пⁱ) - новое множество условных, или "апостериорных", вероятностей.

Если в наше распоряжение поступает новая информация, полученная в результате дополнительных исследований, апостериорные вероятности могут вновь измениться и т.д.

Пример

Допустим, имеет место следующая ситуация. Некоторая торговая фирма продает телевизоры двух марок: "Samsung" (импортные) и "Горизонт" (отечественные). Каждая марка телевизора имеется в двух вариантах - с встроенным телетекстом и без него. Фирма имеет 2 представительства, например, в двух разных городах, каждое представительство получило по 8 телевизоров обеих марок без телетекста и по 6 телевизоров обеих марок с телетекстом. За некоторый отрезок времени одному из торговых представительств фирмы удалось продать 5 телевизоров "Горизонт" без телетекста, 3 телевизора "Горизонт" с телетекстом, 8 телевизоров "Samsung" без телетекста и 5 телевизоров "Samsung" c телетекстом. Другое же представительство продало 5 телевизоров "Горизонт" без телетекста, 1 телевизор "Горизонт" с телетекстом, 6 телевизоров "Samsung" без телетекста и 6 телевизоров "Samsung" c телетекстом.

Ставится задача: определения вероятности продажи телевизора конкретной модели конкретным представительством фирмы.