





















































Введение
Известно, что для кривых втрого порядка в ![]() и для поверхностей второго порядка в
и для поверхностей второго порядка в ![]() имеются основные инварианты,позволяющие однозначно
определить вид и каноническую запись квадрики. Естественно встаёт вопрос,
существуют ли инварианты для поверхностей второго порядка в
имеются основные инварианты,позволяющие однозначно
определить вид и каноническую запись квадрики. Естественно встаёт вопрос,
существуют ли инварианты для поверхностей второго порядка в ![]() , позволяющие однозначно определить вид и каноническую запись
квадрики.
, позволяющие однозначно определить вид и каноническую запись
квадрики.
Целью моей дипломной работы является провести
классификацию поверхностей второго порядка в ![]() используя полную систему инвариантов, а в качестве
конкретного примера привести классификацию поверхностей второго порядка в
используя полную систему инвариантов, а в качестве
конкретного примера привести классификацию поверхностей второго порядка в ![]() . А также разработать элективный курс «Кривые второго
порядка».
. А также разработать элективный курс «Кривые второго
порядка».
Для достижения поставленных целей мною были определены пять задач:
1.
Подробнее
изучить поверхности второго порядка в ![]() , познакомится с их инвариантами.
, познакомится с их инвариантами.
2.
Рассмотреть
способы нахождения канонических уравнений поверхностей второго порядка в ![]() .
.
3.
Провести
классификацию поверхностей второго порядка в ![]() , основанную на значениях
инвариантов.
, основанную на значениях
инвариантов.
4. Применить полученные результаты на практике.
5. Рассмотреть возможность адаптации темы «Кривые второго порядка» для школьников 10-х классов.
Для того чтобы решить поставленные задачи я использовала источники, указанные в списке литературы.
Любая
поверхность второго порядка в ![]() , рассматриваемая как геометрический
объект, не меняется, если от данной декартовой прямоугольной системы координат
перейти к другой декартовой системы координат. Исходное уравнение и уравнение,
полученное после преобразования координат алгебраически эквивалентны.
, рассматриваемая как геометрический
объект, не меняется, если от данной декартовой прямоугольной системы координат
перейти к другой декартовой системы координат. Исходное уравнение и уравнение,
полученное после преобразования координат алгебраически эквивалентны.
Основное значение понятия инварианта: выражение
вида ![]() только в том случае может представлять геометрическую величину,
характерную для самой рассматриваемой поверхности, а не зависящую от случайного
положения осей координат, если это выражение есть инвариант. Поэтому вопрос о
разыскании инвариантов полинома
только в том случае может представлять геометрическую величину,
характерную для самой рассматриваемой поверхности, а не зависящую от случайного
положения осей координат, если это выражение есть инвариант. Поэтому вопрос о
разыскании инвариантов полинома ![]() является одним из самых основных в теории поверхностей второго
порядка.
является одним из самых основных в теории поверхностей второго
порядка.
Моя выпускная квалификационная работа состоит из двух глав. Нумерация формул и рисунков в каждой главе своя.
В первой главе, я рассмотрю определение квадрики
в ![]() , и понятие канонической записи уравнения квадрики. Также
будут рассмотрены преобразования прямоугольной декартовой системы координат в
, и понятие канонической записи уравнения квадрики. Также
будут рассмотрены преобразования прямоугольной декартовой системы координат в ![]() , приводящие к тому, что в новой прямоугольной декартовой
системе координат, квадрика будет иметь наиболее простой вид, канонический. Далее
будут приведены основные инварианты, позволяющие однозначно определить является
ли квадрика центральной, или нецентральной, а также записать каноническое
уравнение квадрики. После этого будет показано практическое применение.
, приводящие к тому, что в новой прямоугольной декартовой
системе координат, квадрика будет иметь наиболее простой вид, канонический. Далее
будут приведены основные инварианты, позволяющие однозначно определить является
ли квадрика центральной, или нецентральной, а также записать каноническое
уравнение квадрики. После этого будет показано практическое применение.
Рассуждения в основном проводятся с использованием записи уравнений в матричной форме, матрицы записаны в блочном виде.
Во второй главе представлен разработанный мной элективный курс «Кривые второго порядка», предназначенный для изучения учащимися 10-х классов. Продолжительность курса – 19 учебных часов. В элективном курсе, гипербола, парабола и эллипс рассмотрены с точки зрения геометрических мест точек, выведены их канонические уравнения и рассмотрены основные свойства. Также материал содержит примерные задания, для решения на практических занятиях, и 3 лабораторные работы с подробным описанием.
Приложение 1 содержит задачи, решенные мной по теме, с использованием материалов выпускной квалификационной работы. Решенные задачи демонстрируют все преимущества использования инвариантов при решение задач данного типа.
Приложение 2 содержит программную реализацию задачи, об определении вида и канонической записи линии второго порядка. Решение реализовано с помощью языка программирования, встроенного в математический пакет Maple.
Глава 1. Поверхности второго порядка
в ![]() мерном
мерном
евклидовом пространстве
1.1. Общее уравнение поверхности второго порядка
Рассмотрим
![]() - мерное евклидовом пространство (
- мерное евклидовом пространство (![]() ) и заданную в нем ортогональную систему
координат с началом в точке
) и заданную в нем ортогональную систему
координат с началом в точке ![]() и базисом
и базисом
![]() .
.
Определение 1: Поверхностью второго порядка (квадрикой) в
![]() -мерном евклидовом пространстве,
называется геометрическое место точек этого пространства, координаты которых, в
какой – либо ортогональной системе координат с началом в точке
-мерном евклидовом пространстве,
называется геометрическое место точек этого пространства, координаты которых, в
какой – либо ортогональной системе координат с началом в точке ![]() и базисом
и базисом ![]() , удовлетворяют алгебраическому уравнению
второй степени относительно
, удовлетворяют алгебраическому уравнению
второй степени относительно ![]() координат
координат ![]() :
:
![]() (1)
(1)
где![]() – группа старших членов (квадратичная форма),
– группа старших членов (квадратичная форма),
![]() – группа членов первой степени (линейная форма),
– группа членов первой степени (линейная форма),
![]() – свободный член.
– свободный член.
Запишем равенство (1) в матричном виде:
![]() (2)
(2)
Здесь обозначено:
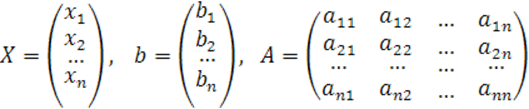
Матрица ![]() - квадратная симметрическая, то есть
- квадратная симметрическая, то есть ![]() . Система координат ортонормированная.
. Система координат ортонормированная.
Определение 2: Если уравнению (1) не удовлетворяет ни одна точка действительного пространства, то поверхность называется мнимой.
Например:
В ![]() , уравнение
, уравнение![]() определяет мнимую окружность.
определяет мнимую окружность.
А в![]() , уравнение
, уравнение ![]() определяет мнимую сферу.
определяет мнимую сферу.
Такие уравнения не имеют геометрического смысла в действительном пространстве, но оно может иметь физический смысл. Также они рассматриваются для сохранения единства терминологии, тем более что не всегда по виду уравнения можно сразу определить задает ли оно мнимую квадрику.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.