Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 7

Выводы

Ранги  и  позволяют определить класс квадрики: при будет центральная квадрика, а при  или  - нецентральная.

Канонические уравнения центральной и нецентральных квадрик имеют вид:

1. 

,

2. 

3. 

где  - ненулевые характеристические числа матрицы ,

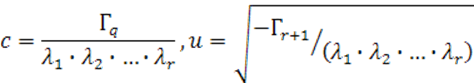
где - инвариант.

Применим вышеизложенный материал на примере:

Привести уравнение квадрики к каноническому виду, определить её  вид.

Решение:

В наших обозначениях имеем

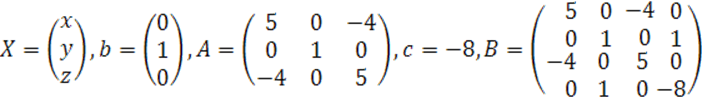
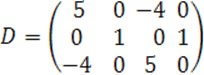
Ранги матриц  определим методом окаймления.

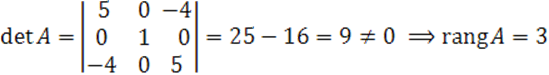
В матрице  возьмем первые три столбца и посчитаем определитель:

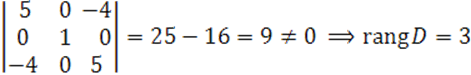
Получили  квадрика центральная каноническое уравнение имеет вид

где

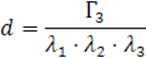
Решим уравнение

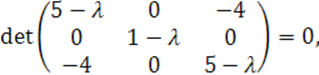
Посчитаем

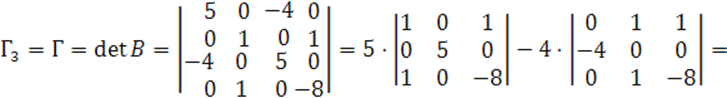
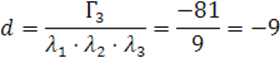
Запишем каноническое уравнение квадрики:

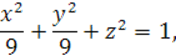
Это уравнение эллипсоида вращения с полуосями  .

Задача решена.

1.6. Классификация квадрик в мерном евклидовом

пространстве

Определение: Невырожденной назовём квадрику, у которой  отличен от нуля.

1.6.1. Классификация центральных квадрик

В случае центральной квадрики  () с уравнением

                           (22)

определитель  матрицы  равен

                                            (23)

В этом случае определитель матрицы  равен

                      (24)

Так как в случае центральной квадрики матрица  имеет обратную, то в случае центральной квадрики определитель  всегда отличен от нуля. Поэтому в том случае, когда центральная квадрика является невырожденной, т.е. , коэффициент

В случае невырожденной центральной квадрики воспользуемся введённым ранее  обозначением

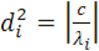                              (25)

Тогда в случае, когда числа имеют одинаковые знаки, противоположные знаку , уравнение (22) можно переписать в виде (26)

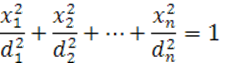
(26)

Эта поверхность  называется эллипсоидом (при уравнение (26) является уравнением эллипса, при  — уравнением эллипсоида

3-х мерного пространства).

В случае, когда числа имеют одинаковые знаки, совпадающие со знаком , уравнение (22) можно переписать в   виде  (27)

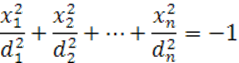
(27)

Данному уравнению  не удовлетворяет ни одна вещественная точка пространства, вследствие чего это уравнение по аналогии с уравнением (26) называют уравнением мнимого эллипсоида (при уравнение  (27) является уравнением мнимого эллипса, при  — уравнением мнимого эллипсоида 3-х мерного пространства).

В случае, когда числа при имеют знаки, противоположные знаку , а при имеют знаки, совпадающие со знаком , уравнение (22) можно переписать в виде (28)

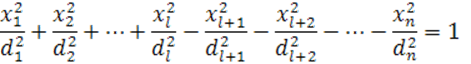
(28)

Поверхность (28) называется гиперболоидом индекса (при  и

уравнение (28) является уравнением гиперболы, при   и  — уравнением однополостного гиперболоида, при   и  — уравнением двуполостного гиперболоида).

Гиперболоид индекса  в - мерном пространстве при  обладает плоскими образующими размерностей , а при  — плоскими образующими размерностей .

В случае вырожденной центральной квадрики () введем обозначения

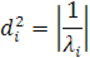
                                       (29)

Тогда в случае, когда числа имеют одинаковые знаки, уравнение (22) можно переписать в виде (30)

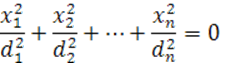
(30)

Уравнению (30) удовлетворяет только одна точка — начало

В случае, когда числа при имеют один знак, а при  — другой знак, уравнение (22) можно переписать в виде (31)

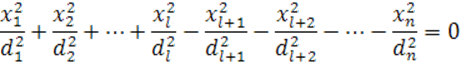
(31)

Так как уравнение (31) однородно, то вместе с точкой этому уравнению удовлетворяют все точки при любом , поверхность (31) называют конусом с вершиной в точке ; этот конус называется конусом индекса , если (случай, когда , приводится к этому случаю умножением всех членов уравнения на ). Уравнение (30) по аналогии с уравнением (31) называют уравнением мнимого конуса с вершиной в точке .

1.6.2. Конусы

Конусы (30) и (31) являются частными случаями конуса с вершиной в точке , определяемого матричным уравнением (32)

                           (32)

которому также вместе с точкойудовлетворяют все точки при любом . Уравнение (32) приводится к виду (30) и (31) в том случае, когда эта квадрика центральная, т. е. .