Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 4

и, следовательно, определитель  матрицы  составленной из коэффициентов  уравнения квадрики, есть инвариант этого уравнения. Порядок инварианта равен .

Определение 2: Многочлен

называется характеристическим многочленом матрицы

Теорема 3. Докажем, что характеристический многочлен матрицы  инвариантен относительно преобразования координат.

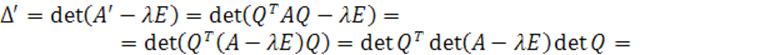
Следствия из теоремы

. Коэффициенты  характеристического многочлена являются инвариантами уравнения квадрики. Они представляют собой суммы главных миноров матрицы соответствующего порядка: инвариант  - это сумма миноров -го порядка, ; в частности,. Порядок инварианта равен .

. Корни характеристического многочлена , то есть характеристические числа матрицы , являются инвариантами уравнения квадрики (Известно, что все  вещественные. [19] или  [10]). Выясним, каков порядок этих инвариантов.

С этой целью рассмотрим характеристические многочлены матриц и , обозначив переменную в первом многочлене через , а во втором –. Эти многочлены таковы: и . Второй многочлен преобразуем:

Таким образом, характеристические числа обеих матриц могут быть найдены из уравнений   и=0. Поэтому они связаны соотношением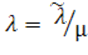. Следовательно, при умножении коэффициентов уравнения квадрики на соответствующие характеристические числа умножаются тоже на . Это значит, что характеристические числа матрицы  являются инвариантами порядка .

Наряду с уже встречавшимися квадратными матрицами и рассмотрим прямоугольную матрицу, у которой строк и  столбцов; соответствующие матрицы, составленные из коэффициентов преобразованного уравнения будем отличать штрихом: В силу (16)

Так как матрицы и неособенные, то ранги матриц равны соответственно рангам матриц. Это значит, что ранги всех трех матриц не меняются при преобразовании координат. Не меняются они и при умножении коэффициентов квадрики на произвольное число. Поэтому ранги матриц   являются инвариантами квадрики.

Перечисленных выше инвариантов недостаточно для полной характеристики квадрики. Квадрика имеет еще один инвариант, не сводящийся к рассмотренным. Обозначим через  определитель -матрицы

.

Этот определитель представляет собой многочлен -ой степени относительно :

.

Здесь  - сумма тех главных миноров го порядка матрицы , которые содержат элемент с, их называют окаймленными минорами матрицы Очевидно что,  ,  .

Теорема

1.  Многочлен  инвариантен относительно поворотов

2.  Если  , то  последних (младших) членов многочлена равны нулю =

3.  Коэффициент , инвариантен при переносах

Доказательство

1.  Первая часть теоремы доказывается непосредственным подсчетом многочлена  в новых координатах. Имеем в силу (16) при

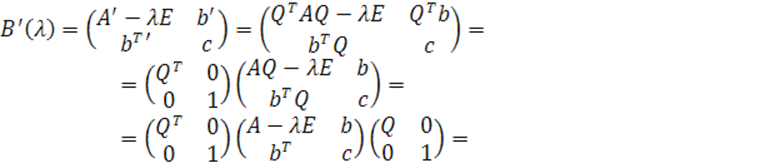
А так как

то .

Инвариантность многочлена  относительно поворотов доказана.

2.  Если , то второе утверждение теоремы тривиально, так как членов, про которые утверждается, что они равны нулю, нет.  Поэтому в дальнейшем будем считать, что . В этом случае имеется  нулевых независимых линейных комбинаций из строк матрицы . Поэтому существует квадратная неособенная матрица порядка , такая, что в матрице первые строк будут нулевыми (здесь имеется ввиду, что существует такое преобразование строк матрицы , что первые  будут нулевыми):

Можно положить  , если это не так, то вместо матрицы  можно взять матрицу . Далее обозначим

и так как , то . Подсчитываем произведение матриц

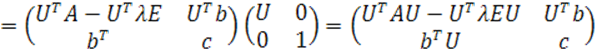       (17)

Выделим нулевые блоки в матрицах и . В матрице-столбце  первые  элементов – нули. Оставшеюся часть обозначим .Так как в матрице  первые  строк тоже нулевые, то и в матрице  первые  строк тоже нулевые, а в силу симметричности последней  матрицы у нее будут нулевыми и первые   столбцов, оставшуюся часть этой матрицы обозначим .Таким образом, получаем:

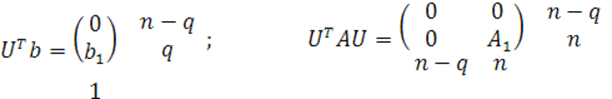
На блоки соответствующих размеров разобьем и матрицу :

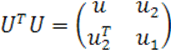
При таких обозначениях из (17) получаем

Поэтому

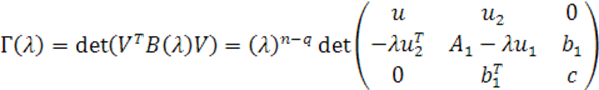   (18)

Таким образом, многочлен  делится на , поэтому члены многочлена, содержащие — в степенях с показателями, меньшими , равны нулю. Этим доказано утверждение (2) теоремы.