В уравнении (1) после приведения подобных содержится
![]() членов.
членов.
Например:
При![]() оно содержит 3 члена, и имеет вид:
оно содержит 3 члена, и имеет вид: ![]() .
.
При ![]() оно содержит 6 членов и имеет вид:
оно содержит 6 членов и имеет вид:
![]() .
.
При ![]() , 10 членов и имеет вид:
, 10 членов и имеет вид: 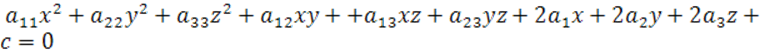
При ![]() – 66 членов.
– 66 членов.
При ![]() – 5151 членов.
– 5151 членов.
Таким образом,
при достаточно больших ![]() , число членов уравнения велико, исследование
поверхности непосредственно по уравнению, написанному в произвольной системе
координат представляет сложность. Поэтому необходимо рассмотреть приемы,
позволяющие уравнение вида (1) привести к каноническому виду.
, число членов уравнения велико, исследование
поверхности непосредственно по уравнению, написанному в произвольной системе
координат представляет сложность. Поэтому необходимо рассмотреть приемы,
позволяющие уравнение вида (1) привести к каноническому виду.
1.2. Преобразование
декартовых прямоугольных координат в ![]()
1.2.1. Перенос начала координат
Пусть
дана декартова система координат с началом в точке ![]() и осями
и осями ![]() . Рассмотрим новую систему координат с
началом в точке
. Рассмотрим новую систему координат с
началом в точке ![]() оси которой
оси которой ![]() , соответственно параллельны осям
, соответственно параллельны осям ![]() старой системы и имеют те же направления
(длина единичных векторов не изменяется). Пусть начало второй системы
старой системы и имеют те же направления
(длина единичных векторов не изменяется). Пусть начало второй системы ![]() имеет координаты
имеет координаты ![]() относительно первой системы координат, а
произвольная точка
относительно первой системы координат, а
произвольная точка ![]() пространства
пространства ![]() имеет координаты
имеет координаты ![]() относительно первой системы и
относительно первой системы и ![]() относительно второй системы, тогда
относительно второй системы, тогда
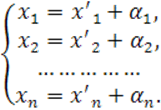 (3)
(3)
или в матричном виде: ![]()
Непосредственным подсчетом найдем результат преобразования в матричном виде:
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() , где
, где
![]()
![]() (4)
(4)
![]()
Введем
матрицы ![]() ,
, ![]() ,
, ![]()
Матрица
![]() получена добавление к матрице
получена добавление к матрице ![]() строки и столбца, а матрица
строки и столбца, а матрица ![]() – матрица преобразования (выражающая
старые координаты через новые).
– матрица преобразования (выражающая
старые координаты через новые).
В силу (4) имеем
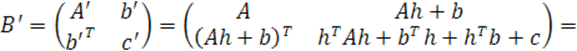
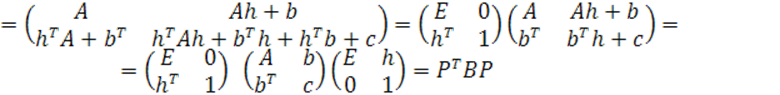
![]()
Теорема
1. Определитель матрицы ![]() и её ранг, а так же матрица
и её ранг, а так же матрица ![]() являются инвариантами относительно
переноса начала координат, т. е.
являются инвариантами относительно
переноса начала координат, т. е.
![]()
Доказательство:
т.к. ![]() , то
, то
![]()
Так
как при умножении на невырожденную матрицу ранг матрицы не изменяется, то
получим ![]() .
.
![]() (равенство 4).
(равенство 4).
Теорема доказана.
1.2.2. Поворот осей, без изменения ориентации системы
базисных векторов
Рассмотрим в
пространстве ![]() две декартовы системы координат. Вторая
получена из первой путем поворота координатных осей. Пусть первая определяется
началом
две декартовы системы координат. Вторая
получена из первой путем поворота координатных осей. Пусть первая определяется
началом ![]() и базисом
и базисом ![]() , а вторая определяется началом
, а вторая определяется началом ![]() и базисом
и базисом ![]() . Пусть нам известны углы, которые образует
каждая ось второй системы с каждой осью первой; обозначения этих углов зададим
таблицей («):
. Пусть нам известны углы, которые образует
каждая ось второй системы с каждой осью первой; обозначения этих углов зададим
таблицей («):
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
Напишем
разложение каждого вектора ![]() по старому базису:
по старому базису:
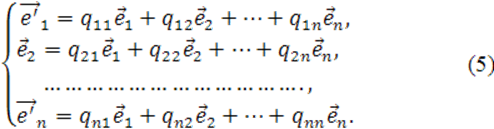
Так как каждый
из векторов ![]() является единичным, то для каждого из них
коэффициентами разложения будут служить направляющие косинусы.
является единичным, то для каждого из них
коэффициентами разложения будут служить направляющие косинусы.
Определение 3.Матрица
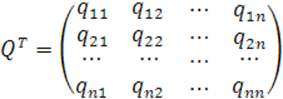
называется матрицей
перехода от базиса ![]() , к базису
, к базису ![]() .
.
В данном случае выполняется равенство:
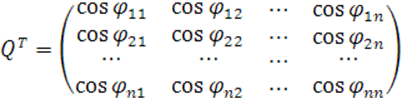 (6)
(6)
Обозначим
через ![]() произвольную точку пространства, через
произвольную точку пространства, через ![]() – старые координаты этой точки, через
– старые координаты этой точки, через ![]() – её новые координаты. Имеет место
векторное равенство:
– её новые координаты. Имеет место
векторное равенство:
![]() (7)
(7)
поскольку его левая и
правая части представляют собой разложение одного и того же вектора![]() (по разным базисам). Заменим в равенстве
(7) векторы
(по разным базисам). Заменим в равенстве
(7) векторы ![]() их выражениями по формулам (5), получим
их выражениями по формулам (5), получим
![]()
![]()
или
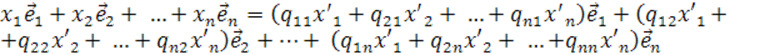 (8)
(8)
Так как коэффициенты разложения вектора по базису однозначно, то из (8) следуют следующие равенства:
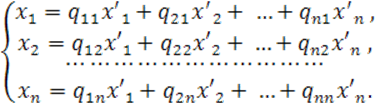 (9)
(9)
Определение 4: Матрица
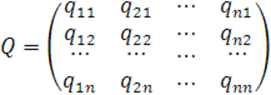
называется матрицей
преобразования координат. Она является транспонированной к матрице ![]() , причем
, причем ![]() тый столбец содержит координаты вектора
тый столбец содержит координаты вектора ![]() относительно базиса
относительно базиса ![]() .
.
Замечание:
![]() и
и ![]() , так как векторы
, так как векторы ![]() и векторы
и векторы ![]() образуют базисы, а это означает, что их
система линейно не зависима.
образуют базисы, а это означает, что их
система линейно не зависима.
Заменим в
формулах (9) коэффициенты ![]() согласно (6), то они примут вид:
согласно (6), то они примут вид:
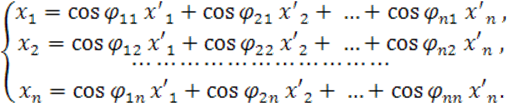 (10)
(10)
Формулы (10) выражают старые координаты произвольной точки через её новые координаты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.