Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 19

Теорема 1. Пусть — точка гиперболы с фокусами . Тогда касательной к гиперболе, проходящей через точку , является прямая, содержащая биссектрису угла .

Доказательство:  Докажем, что прямая , содержащая биссектрису угла , будет касательной к гиперболе (рис. 21). Обозначим .

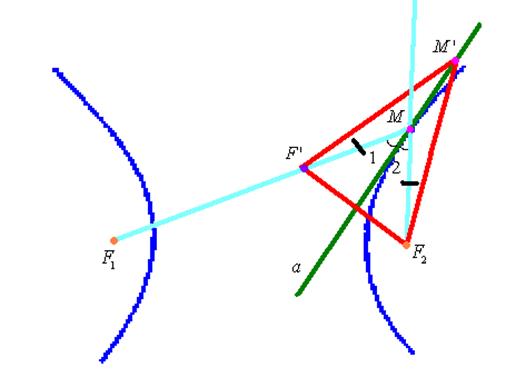
Рис.21.

Рассмотрим точку на прямой , для которой . Тогда прямая будет серединным перпендикуляром к отрезку . Для произвольной точки прямой , отличной от , имеем:

 и . Оценим :

,

Следовательно, . И точка  не лежит на гиперболе.

Следовательно, прямая является касательной.

Фокальное свойство гиперболы: один из фокусов гиперболы, то лучи, отразившись от гиперболы, пойдут так, как будто бы они исходят из другого фокуса.

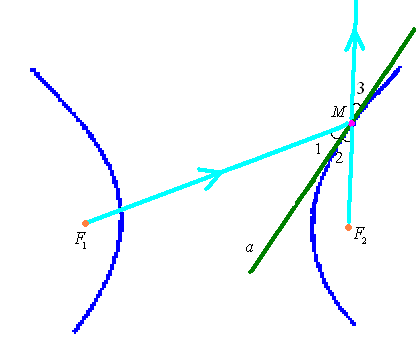
Рис. 22.

2.3.4. Лабораторная работа

«Различные способы получения гиперболы».

Необходимые инструменты: Миллиметровая бумага, ножницы, циркуль, линейка, карандаш, прямоугольник.

Способ 1.  Получение гиперболы из листа бумаги.

Вырежем из листа бумаги круг и отметим точку на оставшейся части листа. Сложим лист так, чтобы эта точка совместилась с какой-нибудь точкой окружности вырезанного круга и на бумаге образовалась линия сгиба. Разогнем лист и снова согнем его, совместив точку с другой точкой окружности. Сделаем так несколько раз. Линии сгибов будут касательными к гиперболе. Граница участка внутри этих сгибов будет иметь форму гиперболы.

Способ 2.

Выберите произвольно числа  и .

Сначала начертим основной прямоугольник ,  используя числа  и , а затем начертим асимптоты гиперболы. (Рис. 23).

На рисунке . Но , а потому . Тогда точки пересечения окружности с центром в точке  и радиусом  определяют фокусы гиперболы . (Рис 24)

Пусть  – некоторое число и . Точки пересечения окружностей с центрами в фокусах и радиусами   и  лежат на гиперболе.

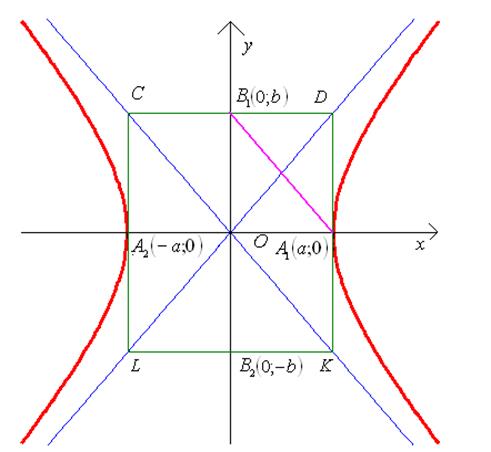
Рис. 23.

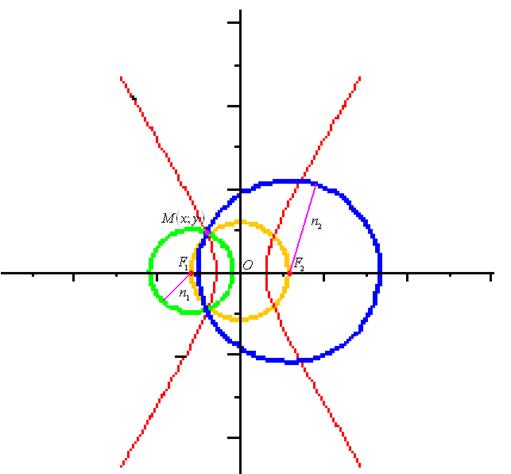
Рис.24.

Меняя число , мы будем получать разные точки гиперболы. А по ним строить искомый график.

Методические рекомендации: На данном занятии, у каждого ученика должны быть все необходимые инструменты и достаточное количество миллиметровой бумаги. Все изображения можно использовать на занятии, для обеспечения наглядности. Также желательно 2 способ предварительно рассмотреть на доске, при помощи проектора. Или снабдить учащихся, подробными инструкциями по выполнению заданий, с использованием изображений. 

2.3.5. Задачи на закрепление материала

1. Записать уравнение гиперболы, если угол между асимптотами равен , а мнимая полуось 4.

2. Выяснить, как влияет эксцентриситет на форму гиперболы.

Решение: В ходе решения задачи №1. был получен важный результат 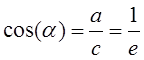, который позволит выявить зависимость между эксцентриситетом и углом между асимптотами ().

Если эксцентриситет будет уменьшаться, то будет возрастать.

Так как , то , следовательно . Если   возрастает, то угол  убывает и стремиться к 0. Следовательно, угол между асимптотами также стремиться к 0.

Если эксцентриситет будет увеличиваться, то будет убывать.

Так как , то , следовательно . Если   убывает, то угол  возрастает и стремиться к прямому. Следовательно, угол между асимптотами стремиться к развернутому.

3.Нарисуйте гиперболу с заданными фокусами  и . Сколько таких гипербол?

4.  Найдите геометрическое место точек пересечения пар окружностей с заданными центрами и разностью радиусов.

5.Ассимптоты гиперболы проходят через начало координат и составляют с осью  углы в . Расстояние между фокусами лежащими на оси , равно 4.

а) Напишите уравнение этой гиперболы в системе координат .

б) Найдите эксцентриситет гиперболы.

в) Напишите уравнения  директрис гиперболы в системе координат .

6. Найдите эксцентриситет  и напишите уравнения директрис гиперболы   ().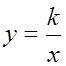

Методические рекомендации: 

Данные задания направлены на закрепление основных понятий связанных с эллипсом (большая и малая полуоси, эксцентриситет, директрисы, фокусы) и установление связей между элементами.

1-4, 6 задачи лучше решить вместе с учащимися на доске. А задачи аналогичные  задаче 5 можно составлять самостоятельно, задавая каждый раз различную пару известных элементов. При решении таких задач, можно применить групповую форму работы.