Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 5

Младший коэффициент многочлена , который может быть отличен от нуля - это . Докажем его инвариантность при переносах. Как отмечалось, при  будет , а инвариантность этого определителя уже доказана. Поэтому, как и в предыдущей части доказательства, считаем . Так как , есть коэффициент многочлена  при , а коэффициенты младших членов равны нулю, то .

Подставив сюда значение из формулы (18), получаем:

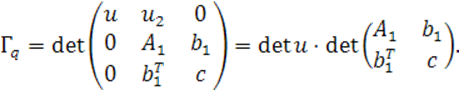              (19)

Для доказательства инвариантности коэффициента  при переносах достаточно подсчитать этот коэффициент в новых координатах и сравнить с (19). В силу (4) имеем:

Поэтому

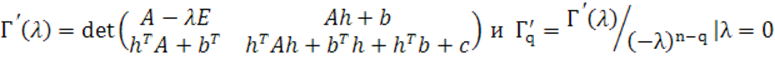
Чтобы подсчитать определитель , выполним в нем два преобразования. Во-первых, первую блочную строку умножим слева на строку и вычтем из второй. Потом первый блочный столбец умножим справа на столбец и вычтем из второго.

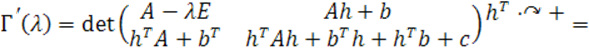
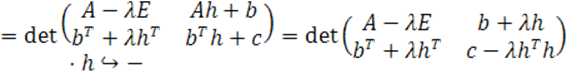
В результате получим:

Во-вторых, полученный определитель представим в таком виде:

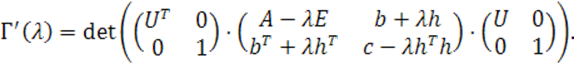
где - матрица, введенная в предыдущей части доказательства.

После умножения получаем:

.

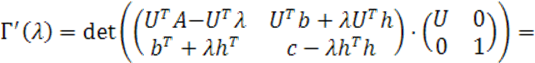
Применяя использованные ранее обозначения блоков матриц  и обозначая дополнительно

можем представить так:

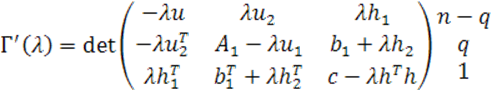
Поэтому

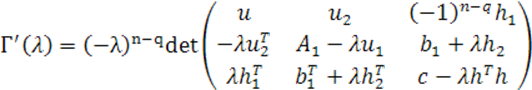
и, следовательно,

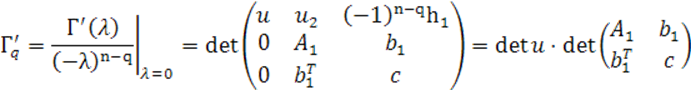
Сравнивая полученный результат с формулой (19), получаем , что и требовалось доказать.

Из доказанной теоремы следует, что есть инвариант уравнения квадрики. Как отмечалось, он представляется в виде суммы миноров

) -го порядка матрицы , поэтому его порядок равен .

1.5. Приведение уравнения квадрики к каноническому виду

В этом параграфе мы найдем канонические уравнения квадрик во всех возможных случаях и выразим их коэффициенты через инварианты.

1.5.1. Центральные и нецентральные квадрики

Выше нами было доказано, что ранг матрицы  и ранг матрицы  являются инвариантами квадрики.   Будем пользоваться обозначениями:

, . Очевидно, что .

Так как матрица отличается от только одним лишним столбцом, то число  либо равно числу , либо на единицу больше. Это позволяет множество всех квадрик разбить на два класса:

Центральные квадрики:  их признак ,

Нецентральные квадрики: их признак  или

1.5.2. Упрощение старших членов уравнения квадрики путем поворота

Попервому уравнению (16) матрица , составленная из коэффициентов старших членов уравнения квадрики, при переходе к новым координатам преобразуется в матрицу , где  - некоторая ортогональная матрица. Из курса линейной алгебры известно, что для любой симметрической матрицы можно так подобрать ортогональную матрицу ,

что матрица  будет диагональной. Легко понять, что диагональные элементы матрицы - это характеристические числа матрицы , которые, как известно, являются инвариантами первого порядка уравнения квадрики. Среди этих характеристических чисел  могут быть нули, количество же ненулевых характеристических чисел равно - рангу матрицы .

Таким образом, получаем:

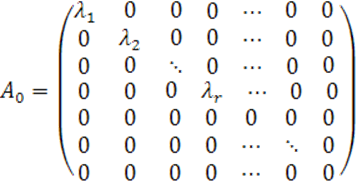
Следовательно, матрица В, составленная из всех коэффициентов уравнения квадрики, в результате такого поворота приводится к следующему виду:

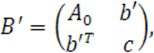               (20)

где столбец определяется второй формулой (14).

Дальнейшие упрощения уравнения квадрики (то есть упрощения ее матрицы) надо выполнять так, чтобы матрица больше не менялась. Вследствие формул (4) это будет, прежде всего, при произвольных переносах. Это будет также и при некоторых поворотах, например, когда ортогональная матрица имеет вид

где  — произвольная ортогональная матрица порядка .

Далее будем отдельно рассматривать преобразование к каноническому виду уравнений центральных и нецентральных квадрик.

1.5.3.Канонические уравнения центральных квадрик

В случае центральной квадрики ранги матриц равны . В силу инвариантности этих рангов это значит, что столбец в матрице (20) есть линейная комбинация столбцов матрицы  . Следовательно, существует такой столбец , что . Выполним теперь перенос . Клетка  , как отмечалось, не изменится, свободный член примет новое значение , а по второй формуле (4) будет . Поэтому матрица квадрики примет следующий (канонический) вид:

а уравнение квадрики –