Другие предметы \ Программирование

Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 17

Также присутствует задача позволяющая связать математику с астрономией. На примере этой задачи. Можно составить множество других. Например, рассчитать эксцентриситеты орбит планет солнечной системы. Желательно воспользоваться справочником по астрономии, чтобы данные задачи были реальные. А так же нужно помнить тот факт, что все планеты солнечной системы движутся по эллиптическим орбитам, в одном из фокусов которых лежит Солнце.

1-4 задачи лучше решить вместе с учащимися на доске. А при решении задач 5-7 можно применить групповую форму работы. После решения задачи 7 необходимо обратить внимание учеников на то, как изменялась малая полуось эллипса, при зафиксированном значении большой полуоси и увеличении эксцентриситета.

2.3. Гипербола

2.3.1. Основные сведения

Определение: Геометрическое место точек плоскости, модуль разности расстояний от которых до двух заданных точек есть величина постоянная, называется гиперболой. Точки называются фокусами гиперболы (рис. 13).

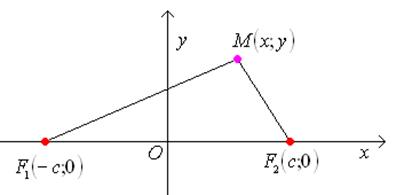
Рис. 13.

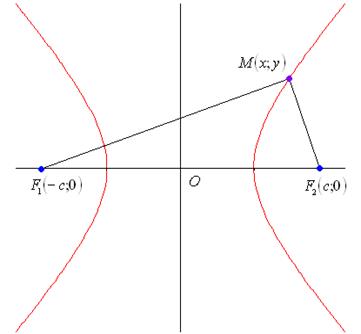
Рис.14. Гипербола

Для точек гиперболы с фокусами выполняется равенство , где — некоторое фиксированное положительное число.

Гипербола состоит из двух ветвей, для точек которых выполняется одно из равенств:

Из неравенства треугольника следует, что должно быть меньше длины отрезка . Обозначим расстояние между фокусами через .

2.3.1.1. Способ изображения

Для того чтобы нарисовать гиперболу, потребуется линейка, нить, длина которой больше длины линейки. Разность длин линейки и нити должна быть меньше, чем расстояние между фокусами. Прикрепим один конец нити к концу линейки, а второй конец к фокусу. Второй конец линейки совместим со вторым фокусом. Натянем нить, прижав ее к линейке острием карандаша (рис. 15). Если поворачивать линейку вокруг фокуса, прижимая к ней карандаш и оставляя нить натянутой, то карандаш будет описывать гиперболу.

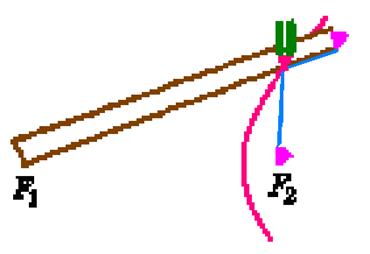
Рис.15. Построение гиперболы

2.3.1. 2. Каноническое уравнение гиперболы

Для вывода уравнения гиперболы выберем систему координат так, чтобы фокусы и лежали на оси , а начало координат совпало с серединой отрезка (см. рис. 13). Тогда фокусы будут иметь координаты и .

Пусть — произвольная точка гиперболы. Тогда согласно определению гиперболы (бескоординатное уравнение гиперболы)или , т. е.

. После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы:

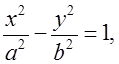(3)

где

2.3.2. Исследование формы гиперболы по ее уравнению.

Установим форму гиперболы, пользуясь ее каноническим уравнением.

1. Уравнение (3) содержит и только в четных степенях.

Следовательно, гипербола симметрична относительно осей и , а также относительно точки , которую называют центром гиперболы.

2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (3), находим две точки пересечения гиперболы с осью : и . Положив в (3), получаем , чего быть не может. Следовательно, гипербола ось не пересекает.