Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 11

Глава 2. Элективный курс «Кривые второго порядка»

2.1. Исторические сведения

2.1.1. Делосская задача

Древнегреческие ученые знали лишь несколько линий, отличных от прямых и окружностей; большинство из них они изучали в связи с тремя знаменитыми задачами древности: об удвоении куба, о трисекции угла и о квадратуре круга. Дошедшая до нас древняя легенда гласит: “Во время страшной эпидемии чумы дельфийского оракула спросили, как умилостивить богов, чтобы они умерили свою ярость. Ответ гласил, что недовольство богов вызвано размерами алтаря, на котором приносят жертвы, боги требуют возвести новый алтарь, вдвое большего объема”. Старый алтарь имел форму куба. Один невежественный стихотворец решил, что достаточно увеличить все его размеры в два раза, чтобы воля богов оказалась выполнимой, он даже воспел в своей поэме новый алтарь. Над невежеством стихоплета смеялись все, поскольку древним грекам было хорошо известно, что если сторону куба увеличить в два раза, то его объем возрастет в восемь  раз.

Если обозначить сторону старого куба через 1, а нового – через , то их объемы равны соответственно  и . “Воля богов” состояла в том, чтобы найти такое , при котором , т.е. . Попытки ученых решить делосскую задачу с помощью циркуля и линейки, т.е. построить отрезок, длина которого равна , к успеху не привели, ибо они пользовались методом геометрических мест, т.е. описывали условия, при которых множество точек образуют нужную кривую. Эти теоретические решения воспринимались с восхищением, поскольку требовали огромного умственного труда.

Полное решение этой задачи оказалось возможным только в IV в. до н.э. Геометр Менехм предложил использовать для этой цели конические сечения. (Если рассматривать конус вращения, то при различном положении секущей плоскости мы будем получать в сечении различные кривые. Тогда в первом случае мы получим кривую – гиперболу, во втором – параболу, в третьем – эллипс. В дальнейшем мы рассмотрим условия, при которых в сечении получается та или иная линия).

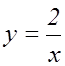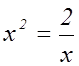Попробуем решить делосскую задачу с помощью параболы и гиперболы, уравнения которых  хорошо известны. Если сторону удваемого куба принять за 1, то выбрав простейшие уравнения параболы  и гиперболы . Составив уравнение , получим . Наглядно  это означает, что абсцисса точки пересечения данных кривых является длиной искомого отрезка, т.е. стороной удвоенного куба.

2.1.2. Кривые второго порядка и законы движения космических тел

Иоганна Кеплера

Современник Галилея Кеплер (1571—1640 гг.), прозванный «законодателем неба», родился в маленьком вюртембергском городке Вейле у бедных родителей. Видимо, его замечательные способности обратили на себя внимание, и он получил возможность поступить в университет. Будучи затем преподавателем математики и других предметов, Кеплер сделался горячим последователем учения Коперника. В 1600 г. Кеплер отправился в Прагу к знаменитому в то время астроному Тихо Браге (1546—1601 гг.), замечательному наблюдателю своего времени, хотя и противнику системы Коперника. Тихо Браге построил на небольшом острове Вен, в 22 км от Копенгагена, роскошную обсерваторию. Телескопов тогда еще не было, а на угломерных приборах наблюдения производились простым глазом. Измерительные инструменты Тихо Браге во многих отношениях усовершенствовал, улучшил он и методы наблюдений. Поэтому за 20 с лишним лет наблюдений и работы на острове Вен он успел собрать богатейший запас весьма точных для того времени наблюдений над положениями планет, комет и звезд.

Тихо Браге понимал, что система Птолемея сложна и плохо вяжется с его очень точными наблюдениями. Однако теорию Коперника, он отвергал. Он придумал свою собственную систему, согласно которой все планеты движутся вокруг Солнца, а само Солнце вместе с ними  движется вокруг Земли.