1. Уравнение
(1) содержит ![]() и
и ![]() только
в четных степенях, поэтому если точка
только
в четных степенях, поэтому если точка ![]() принадлежит
эллипсу, то ему принадлежат точки
принадлежит
эллипсу, то ему принадлежат точки ![]() ,
, ![]() ,
, ![]() . (Это
легко проверить. Если подставить данные координаты точек в уравнение (1), то
будем получать верное равенство. Провести проверку, ученикам лучше
самостоятельно. С целью повторения свойства четных степеней).
. (Это
легко проверить. Если подставить данные координаты точек в уравнение (1), то
будем получать верное равенство. Провести проверку, ученикам лучше
самостоятельно. С целью повторения свойства четных степеней).
Отсюда следует, что эллипс симметричен относительно осей ![]() и
и ![]() , а
также относительно точки
, а
также относительно точки ![]() , которую называют центром
эллипса.
, которую называют центром
эллипса.
2. Найдем
точки пересечения эллипса с осями координат. Положив ![]() ,
находим две точки
,
находим две точки ![]() и
и ![]() , в
которых ось
, в
которых ось ![]() пересекает эллипс (см. рис.7). Положив
пересекает эллипс (см. рис.7). Положив ![]() , находим точки пересечения эллипса с осью
, находим точки пересечения эллипса с осью ![]() :
: ![]() и
и ![]() . Точки
. Точки ![]() ,
,![]() ,
,![]() ,
,![]() называются
вершинами эллипса. Отрезки
называются
вершинами эллипса. Отрезки ![]() и
и ![]() , а также их длины
, а также их длины ![]() и
и
![]() называют соответственно большой и малой
осями эллипса. Числа
называют соответственно большой и малой
осями эллипса. Числа ![]() и
и ![]() соответственно большой и малой полуосями
эллипса.
соответственно большой и малой полуосями
эллипса.
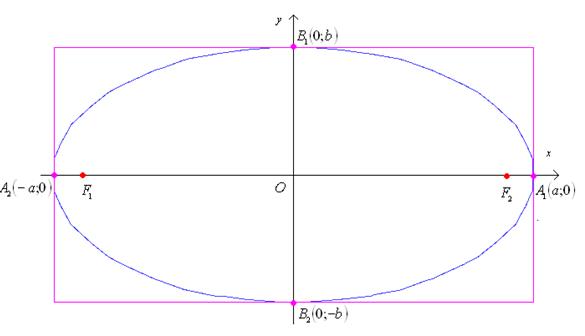
Рис.7.
3. Из уравнения (1) следует, что каждое
слагаемое левой части не превосходит единицы, т.е. имеют место равенства 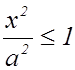 и
и 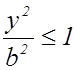 или
или ![]() и
и ![]() .
Следовательно, все точки эллипса лежат внутри прямоугольника, образованного
прямыми
.
Следовательно, все точки эллипса лежат внутри прямоугольника, образованного
прямыми ![]() ,
, ![]() .
.
4. Форма эллипса зависит от отношения![]() . При
. При ![]() эллипс
превращается в окружность, уравнение эллипса принимает вид
эллипс
превращается в окружность, уравнение эллипса принимает вид ![]() . В качестве характеристики формы эллипса
чаще пользуются отношением
. В качестве характеристики формы эллипса
чаще пользуются отношением ![]() .
.
Определение: Отношение ![]() половины
расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом
эллипса и обозначается буквой
половины
расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом
эллипса и обозначается буквой ![]() :
:
![]()
(2)
причем ![]() , так как
, так как ![]() .
.
Приведем формулу (2) к другому виду
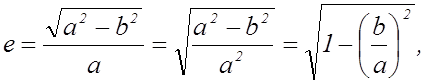
т.е.
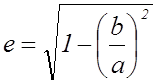 и
и 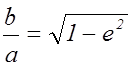 .
.
Отсюда
видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее
сплющенным; если положить ![]() , то эллипс превращается
в окружность.
, то эллипс превращается
в окружность.
Определение:
Пусть ![]() — произвольная
точка эллипса с фокусами
— произвольная
точка эллипса с фокусами ![]() . Длины отрезков
. Длины отрезков ![]() и
и ![]() называются
фокальными радиусами точки
называются
фокальными радиусами точки ![]() . Очевидно,
. Очевидно, ![]() .
.
Определение: Прямые 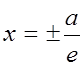 называются директрисами
эллипса. (Рис. 8.)
называются директрисами
эллипса. (Рис. 8.)
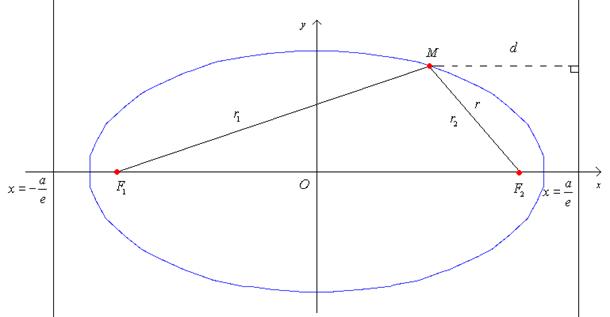
Рис. 8.
Теорема 1. Если ![]() —
расстояние от произвольной точки эллипса до какого-нибудь фокуса,
—
расстояние от произвольной точки эллипса до какого-нибудь фокуса, ![]() — расстояние от
этой точки до соответствующей этому фокусу директрисы, то отношение
— расстояние от
этой точки до соответствующей этому фокусу директрисы, то отношение ![]() , есть постоянная величина, равная
эксцентриситету эллипса:
, есть постоянная величина, равная
эксцентриситету эллипса: 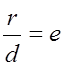 .
.
Определение: Касательной к эллипсу называется прямая, имеющая с эллипсом только одну общую точку.
Теорема 2. Пусть ![]() — произвольная точка эллипса с фокусами
— произвольная точка эллипса с фокусами ![]() . Тогда касательной к
эллипсу, проходящей через точку
. Тогда касательной к
эллипсу, проходящей через точку ![]() , является прямая, содержащая биссектрису угла,
смежного с углом
, является прямая, содержащая биссектрису угла,
смежного с углом ![]() .
.
Доказательство. Докажем, что прямая ![]() содержащая биссектрису
угла, смежного с углом
содержащая биссектрису
угла, смежного с углом ![]() ,
будет касательной к эллипсу (рис. 9). Обозначим
,
будет касательной к эллипсу (рис. 9). Обозначим ![]() .
.
Рассмотрим точку ![]() на прямой
на прямой ![]() , для которой
, для которой ![]() . Тогда прямая
. Тогда прямая ![]() будет серединным перпендикуляром к отрезку
будет серединным перпендикуляром к отрезку ![]() .(Так как треугольник
.(Так как треугольник ![]() - равнобедренный, по построению,
- равнобедренный, по построению, ![]() . Прямая
. Прямая ![]() - биссектриса угла
- биссектриса угла ![]() , следовательно, для
треугольника
, следовательно, для
треугольника ![]() она является медианой и высотой).
она является медианой и высотой).
Для произвольной точки ![]() прямой
прямой ![]() , отличной от
, отличной от ![]() , имеем:
, имеем: ![]() и
и ![]()
Применим «неравенство треугольника» к треугольнику ![]() :
:
![]() .
.
По построению ![]() .
.
Имеем, что ![]()
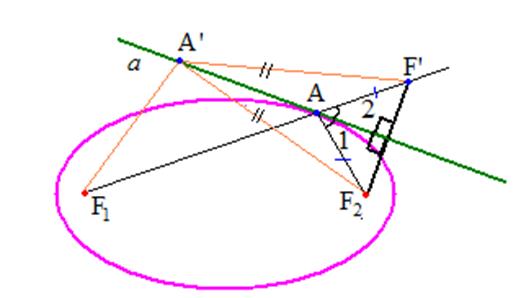
Рис.9.
А
это означает, что точка ![]() не принадлежит эллипсу, следовательно, прямая
не принадлежит эллипсу, следовательно, прямая ![]() имеет только одну общую точку
имеет только одну общую точку ![]() с эллипсом, то
есть является касательной.
с эллипсом, то
есть является касательной.
Фокальное свойство:
Если источник света поместить в один из фокусов эллипса, то лучи, отразившись от эллипса, соберутся в другом его фокусе.
Воспользуемся тем, что угол падения света равен углу отражения, и тем, что от кривой свет отражается так же, как от касательной, проведенной в точку падения.
2.2.3. Лабораторная работа
«Различные способы получения эллипса»
Необходимые инструменты: Бумага, ножницы, циркуль, линейка, карандаш, картон, сковорода, прямоугольник.
Способ 1.
Получения эллипса из листа бумаги.
Вырежем из бумаги большой круг и в любом его месте, отличном от центра, поставим точку F.
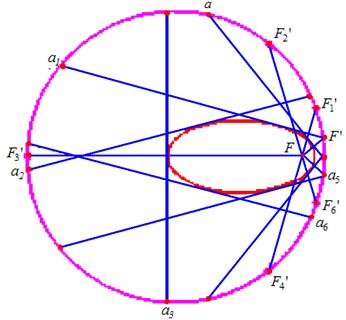
Рис.10.
Сложим
круг так, чтобы эта точка совместилась с какой-нибудь точкой F' окружности круга и на бумаге
образовалась линия сгиба ![]() (рис. 10). Линия сгиба будет серединным перпендикуляром к
отрезку FF' и, следовательно, касательной к эллипсу. Разогнем круг и снова
согнем его, совместив точку Fс другой точкой окружности круга. Сделаем так несколько
раз, пока вся бумага не покроется линиями сгибов. Линии сгибов будут
касательными к эллипсу. Граница участка внутри этих сгибов будет иметь форму
эллипса.
(рис. 10). Линия сгиба будет серединным перпендикуляром к
отрезку FF' и, следовательно, касательной к эллипсу. Разогнем круг и снова
согнем его, совместив точку Fс другой точкой окружности круга. Сделаем так несколько
раз, пока вся бумага не покроется линиями сгибов. Линии сгибов будут
касательными к эллипсу. Граница участка внутри этих сгибов будет иметь форму
эллипса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.