Приведенный выше материал написан, прежде всего, для учителя. Большинство сведений учащиеся в состоянии найти сами, а учитель может дополнить сведения найденные учениками. И в конце занятия подвести итог всему сказанному.
Все используемые в тексте рисунки, можно использовать для составления презентации в PowerPoint. Что позволит сделать рассказ более наглядным и интересным.
2.2. Эллипс
2.2.1. Основные сведения
Определение: Геометрическое место точек (ГМТ)– фигура, которая состоит из всех точек плоскости, обладающим определенным свойством.
Например, окружность – ГМТ равноудаленных от данной точки (центра).
Эллипс, по-видимому, был известен еще в глубокой древности, когда облик геометрии соответствовал дословному переводу ее названия. В те времена основными инструментами для выполнения построений на местности были колья и веревки, позволявшие проводить прямые и окружности, а значит, и выполнять те построения, которые теперь называют построениями с помощью циркуля и линейки.
Ясно, как с помощью указанных инструментов построить окружность: нужно закрепить один из концов веревки и в натянутом состоянии прочертить вторым концом линию.
А что получиться, если закрепить оба конца ненатянутой веревки, а затем в натянутом состоянии прочертить линию? Получиться эллипс.
Определение: Геометрическое место точек плоскости, сумма расстояний от
которых до двух заданных точек 
, 
есть величина постоянная, называется эллипсом. Точки
, называются фокусами эллипса.
Обозначим расстояние между фокусами через 
, а сумму расстояний от произвольной точки эллипса до
фокусов – через 
.(Рис. 4)
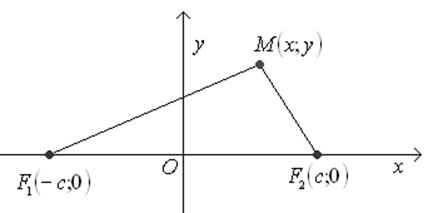
Рис. 4.
Из неравенства треугольника следует, что
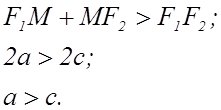
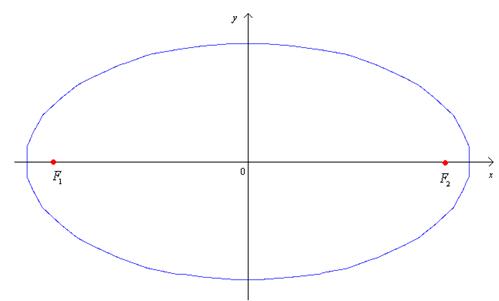
Рис. 5. Эллипс.
Слово «фокус» в переводе с латинского языка означает
«очаг», «огонь», и именно это свойство эллипса послужило основанием для
названия точек 
фокусами.
Для того чтобы нарисовать эллипс, потребуется нить и кнопки. Прикрепим концы нити к фокусам. Карандашом натянем нить так, чтобы его острие касалось бумаги. Будем перемещать карандаш по бумаге так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге эллипс (рис. 6).
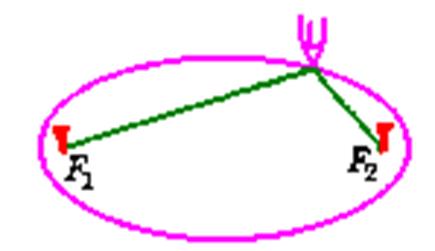
Рис. 6. Способ построения эллипса
Для
вывода уравнения эллипса выберем систему координат 
так,
чтобы фокусы и лежали
на оси 
, а начало координат совпадало с серединой
отрезка 
. Тогда фокусы будут иметь следующие
координаты: 
и 
. (см.
рис 4).
Пусть
– произвольная точка эллипса. Тогда,
согласно определению эллипса, 
(данное равенство
называется
бескоординатным уравнением эллипса),
т.е. 
.
Данное уравнение и является уравнением эллипса, но его можно
преобразовать к более простому виду, если положить 
.
И тогда наше уравнение примет вид:
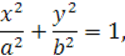(1)
Оно называется каноническим уравнением эллипса.
Методические рекомендации:
Вывод уравнения эллипса не является задачей данного курса, поэтому сама процедура вывода не приведена. Но в тоже время намечен путь получения канонического уравнения. Это можно использовать с целью активизации познавательной деятельности учащихся. Большинство учеников заинтересуются выводом и попробуют довести преобразования до конца, тем более они им посильны. Это позволит не тратить время на занятии на вывод формулы, и дать возможность учащимся проявить активность и самостоятельность. В качестве задания это можно не проговаривать, но на следующем занятии спросить: «Ребята, кто-нибудь довел дело до конца? Вы убедились в правильности конечного результата». После такого вопроса, даже те, кто изначально не проявлял интерес, заинтересуются. А если еще у некоторых учеников получатся разные результаты, то это повлечет за собой споры и обсуждения. На данном этапе учитель может предложить свою помощь. Поэтому доведем вывод до конца.
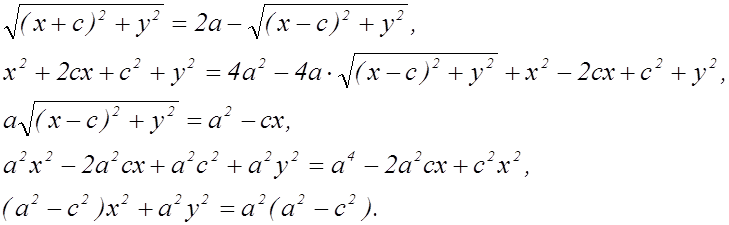
Так как 
, то 
. Положим 
.
Тогда последнее уравнение примет вид 
или
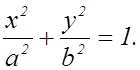
2.2.2. Исследование формы эллипса по его уравнению
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.