Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 23

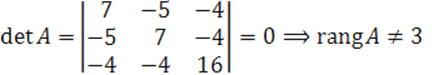
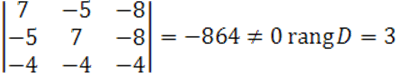
Получили  квадрика нецентральная каноническое уравнение имеет вид

где

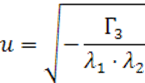
Решим уравнение

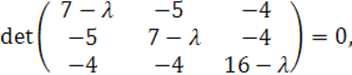
Посчитаем

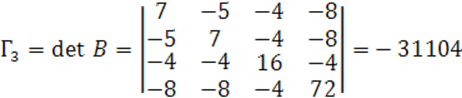
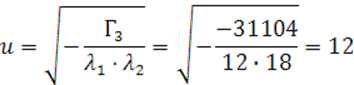
Запишем каноническое уравнение квадрики:

Это уравнение эллиптического параболоида. Задача решена.

5.   

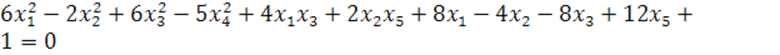в

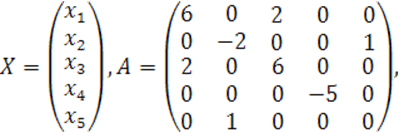
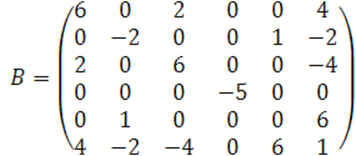
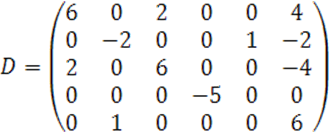
Ранги матриц  определим методом окаймления.

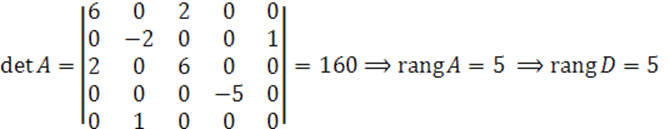
Получили  квадрика центральная каноническое уравнение имеет вид

где

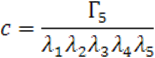
Решим уравнение

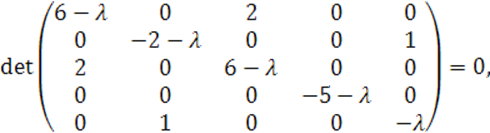
Посчитаем

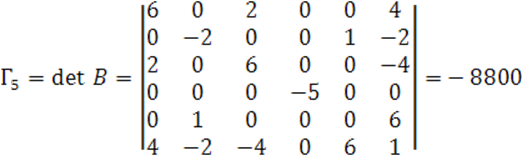
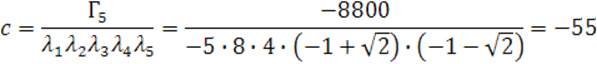
Запишем каноническое уравнение квадрики:

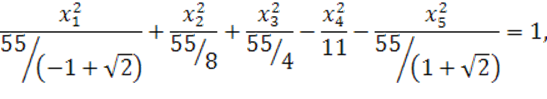
Это уравнение гиперболоида индекса 3. Задача решена.

Приложение 2.

Задача определения типа квадрики и её канонического уравнения, была реализована программно, при помощи мощного математического пакета Maple, для программирования использовался встроенный язык программирования.

Текст программы:

KPV:=proc(a, b, c, d, e, f)

local W,T,V,k,A1,A2,l;

globalDelta, delta, p, S, H, lambda1, lambda2, kz, solutions;

S:=a+c;

Delta:=linalg:-det(linalg:-matrix([[a,b,d],[b,c,e],[d,e,f]]));

delta:=linalg:-det(linalg:-matrix([[a,b],[b,c]]));

W:=S*Delta;

H:=linalg:-det(linalg:-matrix([[c,e],[e,f]]))+linalg:-det(linalg:-matrix([[a,d],[d,f]]));

if 0<delta then

T:=’Эллиптический’;

ifDelta=0 then

V:=’Совокупность двух мнимых непараллельных сопряженных прямых’

else

if 0<W then V:=’Мнимыйэллипс’ else V:=’Эллипс’  end if

end if

else

if delta=0 then

T:=’Параболический’

ifDelta=0 then

if H=0 then

                    V:=’Совокупность двух действительных совпадающих прямых’

else

if 0<Hthen

V:=’Совокупность двух мнимых параллельных прямых’

else

V:=’Совокупность двух различных действительных прямых’

end if

end if

                    else

          V:=’Парабола’

                    end if

else

T:=’Гиперболический’;

                    ifDelta=0thenV:=’Совокупность двух действительных пересекающихся прямых’ elseV:=’Гипербола’ endif

end if

end if;

p:=lambda^2-S*lambda+delta;

solutions:=[solve(p,lambda)];

lambda1:=solutions[1];

lamda2:=solutions[2];

if V=’Эллипс’ then

if abs(lambda2)<abs(lambda1) then l:=lambda1; lambda1:=lambda2; lambda2:=l end if;

          k:=Delta/delta;

          kz:={-x^2*lambda1/k-y^2*lambda2/k=1}

end if;

if V=’Мнимыйэллипс’ then

 ifabs(lambda2)<abs(lambda1)then l:=lambda1; lambda1:=lambda2; lambda2:=l end if;

          k:=Delta/delta;

          kz:={-x^2*lambda1/k-y^2*lambda2/k=-1}

end if;

if V=’Парабола’ then kz:={y^2=2sqrt(-Delta/S^3)*x} end if;

ifV=’Совокупность двух действительных пересекающихся прямых’ then

if (lambda1-lambda2)*b<0 then l:=lambda1; lambda1:=lambda2; lambda2:=l

end if;

          kz:={lambda1*x^2+lambda2*y^2=0}

endif;

ifV=’Совокупность двух мнимых непараллельных сопряженных прямых’ then

if (lambda1-lambda2)*b<0 then l:=lambda1; lambda1:=lambda2; lambda2:=l

end if;

kz:={lambda1*x^2+lambda2*y^2=0}

endif;

ifV=’Совокупность двух различных действительных параллельных прямых’ or‘Совокупность двух мнимых параллельных прямых’ then

kz:={y^2+H/S^2=0}

end if;

ifV=’Совокупность двух действительных совпадающих прямых’ then

kz:={y^2=0}

endif;

print(‘Тип’=T, ’Delta’=Delta, ’delta’=delta, ’p’=p, ’lambda1’=lambda1,       ’lambda2’=lambda2, ‘Вид’=V, ‘Каноническая запись’=kz)

end proc

Блок-схема

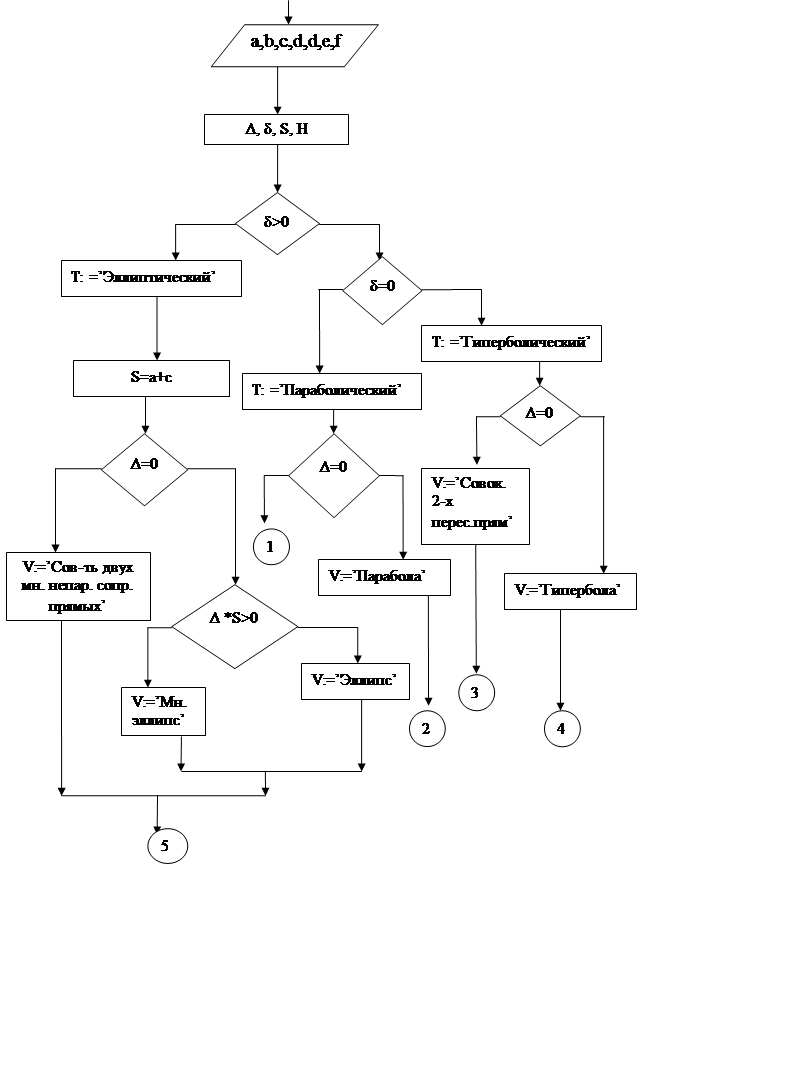
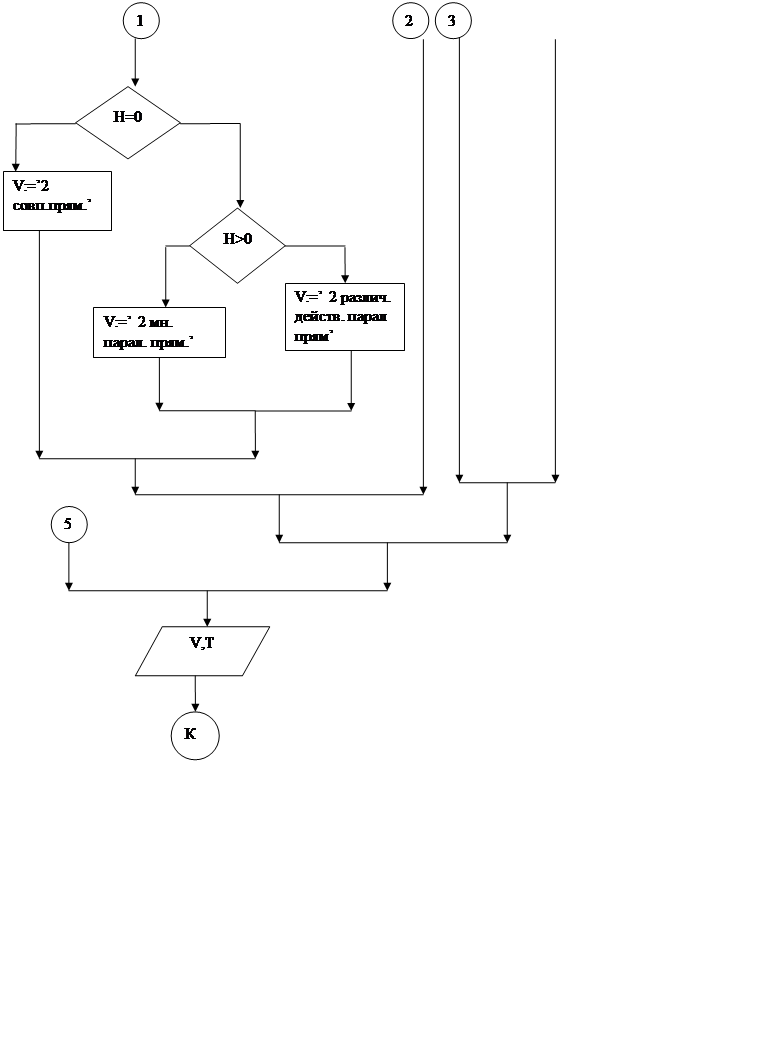
Результат работы

KVP(9,-6,4,0,0,39);

Тип=Параболический, Δ=0, δ=0, , Вид=Совокупность двух мнимых параллельных прямых, Каноническая запись={}

KVP(9,-12,16,-10,55,-50);

Тип=Параболический, Δ=-15625, δ=0, , Вид=Парабола, Каноническая запись={}

KVP(5,-3,5,0,0,16);

Тип=Эллиптический, Δ=256, δ=16, , Вид=Мнимый эллипс, Каноническая запись=

Заключение

Поставленные мной задачи, были выполнены в процессе изучения теоретического материала. Была составлена  таблица, в которой приведена классификация поверхностей второго порядка в 4-х мерном евклидовом пространстве.

Также был разработан элективный курс «Кривые второго порядка», предназначенный для учащихся 10 классов.