Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 16

Способ 2.  

Данный способ, можно рассмотреть всем вместе. Для того чтобы можно было воспользоваться одной сковородой.

Получение эллипса с использованием сковороды и картонного круга, диаметром вдвое меньшим диаметра сковороды.

Клейкой лентой укрепим на дне сковороды лист бумаги. Положив круг на сковороду, продырявим его в любом месте, отличном от центра, отточенным карандашом. Если теперь катить круг по краю сковороды, прижимая острие карандаша к бумаге, то на бумаге появится эллипс.

Способ 3.

Проведем окружности  и  с центром в начале координат и с радиусами соответственно  и  (Рис.11).

Пусть луч  пересекает окружности   и   соответственно в точках  и . Допустим, что  — проекция точки  на ось абсцисс, — проекция точки  на ось ординат,   — точка пересечения прямой, проходящей через   и параллельной , с прямой, проходящей через  и параллельной .

Точка  лежит на эллипсе. Аналогично можно построить ряд других точек эллипса, а затем, используя найденные точки, построить полностью его график.

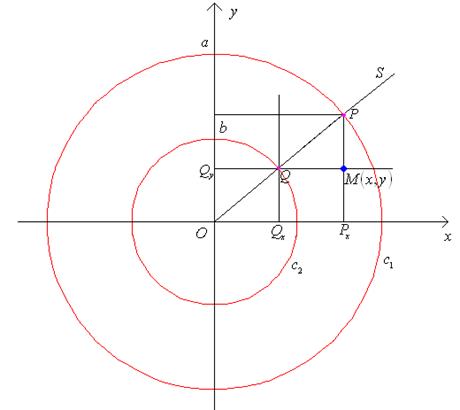
Рис. 11.

Способ 4.

Сначала строим вершины .  Затем находим фокусы  и  как точки пересечения окружности с радиусом с центром в точке  с осью абсцисс. Точку  определим как пересечение окружности радиуса  с центром в точке  и окружности радиусом  с центром в , где  — произвольное положительное число, заключенное между  и  (Рис. 12).

Используя ряд точек, построенных указанным способом, можно построить полностью график эллипса.

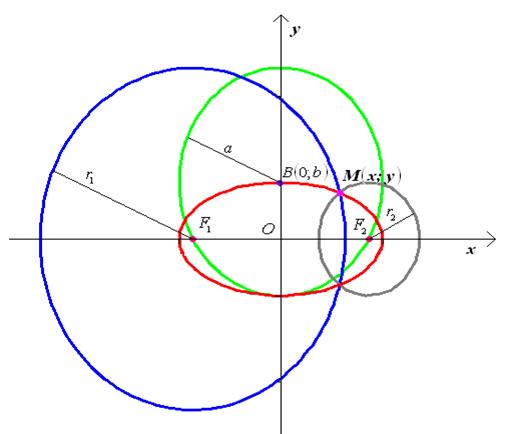
Рис.12.

Методические рекомендации: На данном занятии, у каждого ученика должны быть все необходимые инструменты и достаточное количество бумаги и картона. Все изображения можно использовать на занятии, для обеспечения наглядности. Также желательно 3 и 4 способ предварительно рассмотреть на доске, при помощи проектора. Или снабдить учащихся, подробными инструкциями по выполнению заданий с использованием изображений. 

2.2.4. Задачи на закрепление материала

1.  Нарисуйте эллипс с заданными фокусами . Сколько таких эллипсов?

2.  Что будет происходить с эллипсом, если эксцентриситет:

а) будет увеличиваться

б) уменьшаться?

Решение:

а) если эксцентриситет будет увеличиваться;

Зафиксируем . Пусть , т.е. 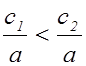, следовательно .  и   . Следовательно .

Вывод: При увеличении , расстояние между фокусами растёт, а малая полуось эллипса уменьшается. В предельном случае получим, что эллипс сожмется в отрезок.

б) если эксцентриситет будет уменьшаться;

Зафиксируем . Пусть , т.е. 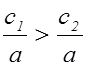, следовательно .  и   . Следовательно .

Вывод: При уменьшении , расстояние между фокусами уменьшается, а малая полуось эллипса увеличивается. В предельном случае получим, что эллипс превратиться в окружность. Так как если ,  то , и фокусы совпадут.

3.  Наибольшая высота спутника над Землей 700 км, а наименьшая   200 км. Найти эксцентриситет орбиты.

4.  Для заданных точек и найдите геометрическое место точек , для которых периметр треугольника   равен постоянной величине .

5.  Леонардо да Винчи (1452-1515) предложил следующий способ построения эллипса. Вырежем из бумаги произвольный треугольник . Проведем на листе бумаги две прямые  и , Будем прикладывать треугольник  так, чтобы вершина  принадлежала прямой , вершина — прямой , отмечая всякий раз на бумаге, положение вершины . Различные положения вершины будут заполнять эллипс. Проверьте.

6.  Расстояние между двумя фокусами эллипса равно , а отношение большой и малой полуосей равно 3.

а) Напишите уравнение этого эллипса в системе координат , где – середина отрезка, соединяющего фокусы, лежащие на оси .

б) Найдите эксцентриситет эллипса.

в) Напишите уравнения директрис эллипса в системе координат .

7.  Написать уравнение эллипса если , а .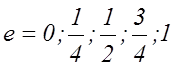

Методические рекомендации: 

Данные задания направлены на закрепление основных понятий связанных с эллипсом (большая и малая полуоси, эксцентриситет, директрисы, фокусы) и установление связей между элементами.