Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 3

Запишем обратные формулы, выражающие новые координаты через старые. Чтобы это сделать достаточно в формулах (9) поменять ролями старые и новые координаты, одновременно транспонируя таблицы («) и (6). В результате получим:

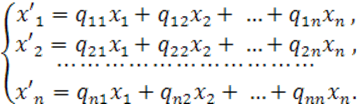             (11 a)

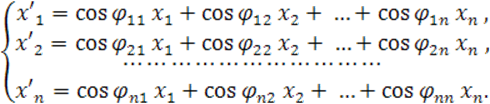        (11 b)

Замечание:

Выясним, каким условиям удовлетворяют коэффициенты  в формулах (9).

Так как новые базисные векторы  являются единичными, поэтому из формул (11а) имеем:

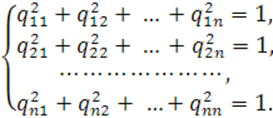                    (12)

Векторы  попарно перпендикулярны друг к другу, поэтому их попарно взятые скалярные произведения равны нулю:

                                 (13)

Тогда имеем

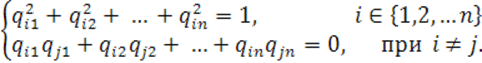
а это означает, что матрица  ортогональная.

Пусть  ортогональная матрица порядка  (то есть ). Запишем равенство (9) в матричном виде:

Непосредственным подсчетом найдем результат преобразования в матричном виде:

,

, где

                                                                                   (14)

Введем матрицы  ,  ,

Матрица  получена добавление к матрице строки и столбца, а матрица     – матрица  преобразования (выражающая старые координаты через новые).

В силу (14) имеем  

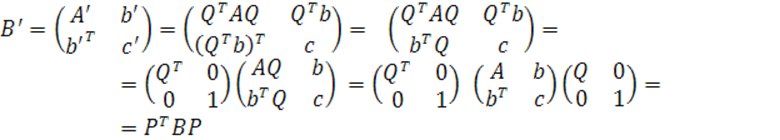
Теорема 2. Определители матриц  и  и их ранги, являются инвариантами относительно поворота системы координат, т. е.

Доказательство: т.к. , то

Так как при умножении на невырожденную матрицу ранг матрицы не изменяется, то получим  . т.к. , то

Так как при умножении на невырожденную матрицу ранг матрицы не изменяется, то получим  .

Теорема доказана.

1.3. Канонический вид уравнения квадрики

Пусть квадрика в некоторой декартовой системе координат задана уравнением (1). Упростим это уравнение путем надлежащего выбора новой декартовой системы координат.

Уравнение преобразования системы координат в матричном виде:

,                            (15)

где  координатные столбцы текущей точки в старых и новых координатах,  – ортогональная матрица порядка , – столбец высоты .

Данное уравнение задает поворот и перенос системы координат. При   преобразование координат называется переносом,  – поворотом.

Непосредственным подсчетом найдем результат преобразования в матричном виде:

,

, где

                                                                                 (16)

Известно, что путем определенного выбора преобразования координат уравнение (1) можно привести к каноническому виду:  

, где .    ([14])

1.4. Основные инварианты

Определение 1: Ортогональный инвариант уравнения квадрики - это такая функция   коэффициентов ее уравнения, которая не меняется при преобразовании данной ортонормированной системы координат к другой ортонормированной системе с базисными векторами той же длины, то есть при преобразовании уравнения (2) по формуле (15).

Инвариант уравнения квадрики может изменяться при умножении всех коэффициентов уравнения (2) на одно и то же число , то есть, вообще говоря, . Во многих случаях инварианты являются однородными функциями коэффициентов уравнения квадрики. В таких случаях

Число   - степень однородной функции - будем называть порядком инварианта. При   инвариант уравнения квадрики будет инвариантом самой квадрики. Такой инвариант имеет геометрический смысл.

Пусть - инварианты уравнения квадрики порядков , а  - какие-либо числа;  Тогда   есть тоже инвариант уравнения квадрики, а его порядок равен  .

Далее мы рассмотрим ряд инвариантов уравнения квадрики, которые позволяют во всех случаях записать каноническое уравнение квадрики. Они образуют полную систему инвариантов уравнения квадрики.

Докажем в общем случаи (для преобразования 15) что .

Так как   и , то имеем

Таким образом, определитель  матрицы , составленной из коэффициентов старших  членов уравнения квадрики, есть инвариант ее уравнения. Легко видеть, что порядок этого инварианта равен .

Рассмотрим матрицы :

,

Введем еще одну матрицу того же порядка:

Покажем, что  

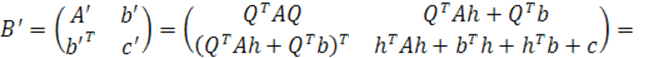
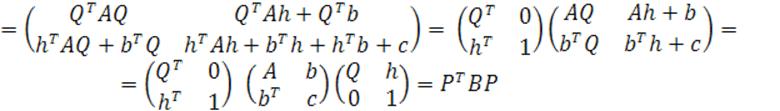
Так как   и , то