Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 6

                           (21)

При   это уравнение часто записывают в такой форме:

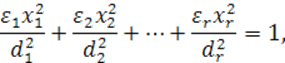
где опущены штрихи упеременных и обозначено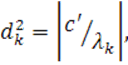

.

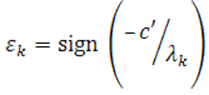Осталось выразить коэффициенты уравнения (21) через инварианты. Собственно, выразить осталось только так как инвариантность характеристических чисел  доказана ранее.

Подсчитаем для канонической матрицы  инвариант  (для центральных квадрик ). Это будет сумма окаймленных миноров -го порядка матрицы . Из этих миноров отличным от нуля может быть только один, поэтому

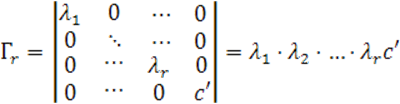
Откуда .

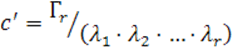Видим, что  - инвариант первого порядка уравнения квадрики, как и характеристические числа . Поэтому  и  - инварианты порядка , то есть инварианты самой квадрики. Обычно  называют полуосью квадрики, причем при - вещественной, а при  - мнимой.

1.5.4.   Канонические уравнения нецентральных квадрик

Возвратимся к матрице (20), полученной в результате преобразования уравнения квадрики путем надлежащим образом подобранного поворота.

Рассмотрение данного вида квадрик разобьём на 2 части, сначала рассмотрим квадрики удовлетворяющие условию , а затем условию .

1.

В данном случае столбец не может быть представлен в виде линейной комбинации столбцов матрицы , поэтому он не может быть уничтожен переносом.

Блочную матрицу (20) разобьем на более мелкие блоки:

где

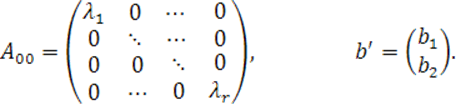
После этого упрощение матрицы осуществим в три шага.

Шаг 1. Так как  - неособенная матрица, то существует столбец  высоты   такой, что  . Заметив это, выполним перенос

, где

При этом в соответствии с (4) столбец  преобразуется в столбец

, свободный член примет новое значение , а остальные блоки матрицы не изменятся. Поэтому матрица квадрики в результате первого шага примет следующий вид:

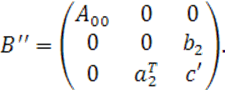
Отметим, что столбец   обязательно отличен от нулевого так как в противном случае квадрика не  удовлетворяла бы условию .

Шаг 2. Прежде чем выполнить следующее преобразование, докажем, что существует такая ортогональная матрица порядка  , что в столбце все элементы, кроме последнего, будут нули.

Для этого в -мерном евклидовом пространстве , в котором введен ортонормированный базис, рассмотрим вектор с координатным столбцом Длину вектора  обозначим , то есть. В этом же пространстве рассмотрим вектор с координатным столбцом

; длина этого вектора тоже равна .

Ясно, что существует ортогональное преобразование пространства , преобразующее вектор  в вектор . Это вытекает, например, из того, что каждый из этих векторов можно дополнить до ортонормированного базиса, а линейное преобразование, отображающее один из этих базисов на другой, - ортогональное. Отсюда следует, что существует такая ортогональная матрица порядка , что .

Теперь возвратимся в исходное пространство  и выполним в нем преобразование системы координат (поворот) по формуле  , где

В соответствии с формулами (14) получим матрицу квадрики в новых координатах:

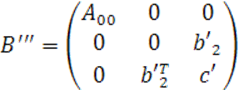
или, возвращаясь к блокам прежних размеров,

.

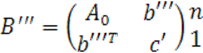где

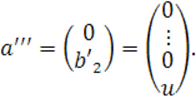
Шаг 3. Теперь можно переносом  уничтожить свободный член , для чего достаточно столбец взять таким:

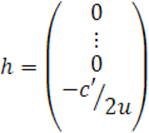, в этом убеждаемся с помощью последней формулы (16). Другие же блоки матрицы квадрики не меняются.

Окончательно получаем:

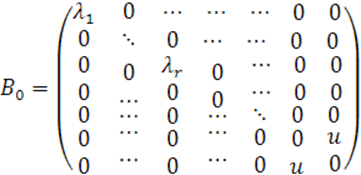
Этой матрице соответствует каноническое уравнение нецентральной квадрики

  (22)

которое можно записать и в форме

здесь опущены штрихи у переменных и обозначено

Остается выразить коэффициент через инварианты. Инвариант  () есть сумма окаймленных главных миноров -го порядка матрицы . Но отличен от нуля лишь один такой минор - это минор, образованный  первыми и двумя последними столбцами и строками матрицы . Поэтому

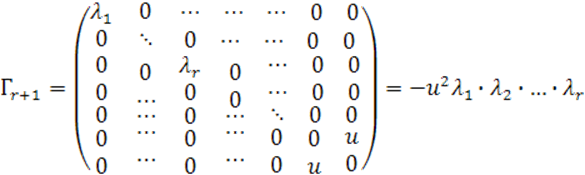
откуда 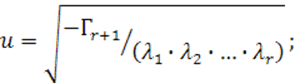  мы берем положительное значение корня, но можно было бы взять и отрицательное, так как на втором шаге вектор можно заменить на вектор. Отсюда видим, что - инвариант первого порядка уравнения квадрики, а  и  - инварианты самой квадрики.

2.

В данном случае будем проводить рассуждения, аналогичные тем, которые были проведены для центральной поверхности, за тем исключением, что для записи канонического уравнения будем рассматривать поверхность не в , а в . Но название поверхности будем определять учитывая, что мы находимся в