В настоящее время три закона, установленные Кеплером, обычно формулируются следующим образом:
Первый закон. Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.
Второй закон. Радиус-вектор планеты в равные времена описывает равные площади.
Третий закон. Квадраты времен сидерических обращений различных планет вокруг Солнца пропорциональны кубам больших полуосей их орбит.
По эллипсам движутся не только планеты, но и их естественные и искусственные спутники. Ближайшая к Земле точка орбиты Луны или какого-нибудь искусственного спутника Земли называется перигеем (греч. Гея или Те — Земля), а наиболее удаленная — апогеем. У орбит искусственных спутников Луны соответствующие точки получили названия периселений (греч. Селена — Луна) и апоселений.
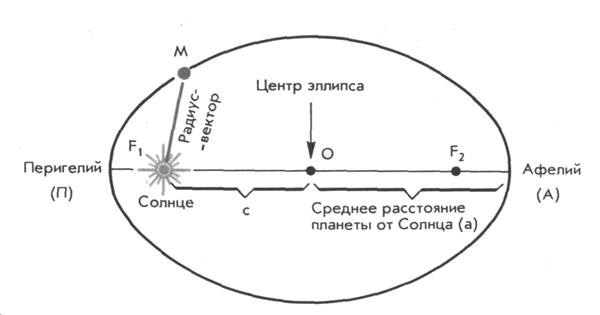
Рис. 1. Орбита планеты – эллипс.
Из того, что площади, описываемые радиус-вектором в одинаковые промежутки времени, равны, следует, что соответствующие дуги орбиты неодинаковы и линейная скорость на орбите меняется так, что наибольшую скорость планета имеет в перигелии, а наименьшую — в афелии.
Рисунок 2 иллюстрирует второй закон Кеплера.
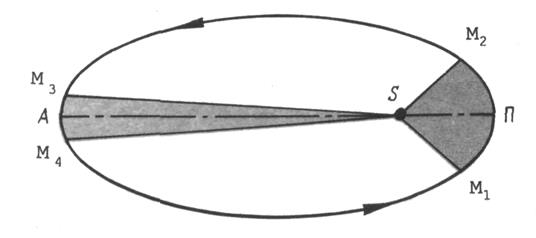
Рис. 2. Второй закон Кеплера.
Из формулы третьего закона
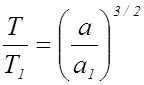или 
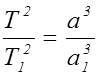, следует,
что если 
(году) и 
(среднему расстоянию Земли от Солнца), то
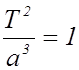.Мы видим, что отношение квадрата сидерического периода
обращения любой планеты к кубу ее среднего расстояния от Солнца должно быть
постоянно и равно единице или очень близко к единице, если период обращения
выражается в годах, а расстояние — в астрономических единицах.
Строго эллиптическое движение происходит под действием притяжения одного тела. Но любая планета испытывает притяжение со стороны других планет, своих спутников и т. д. В результате возникают отклонения от эллиптической траектории, которые называются в небесной механике возмущениями.
Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения. Он доказал, что под действием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе. В этом заключается первый обобщенный Ньютоном закон Кеплера. Он имеет универсальный характер и справедлив для любых тел, между которыми действует взаимное тяготение. Ему подчиняется и движение искусственных небесных тел.
Форма орбиты зависит от модуля и направления начальной скорости (рис.3).
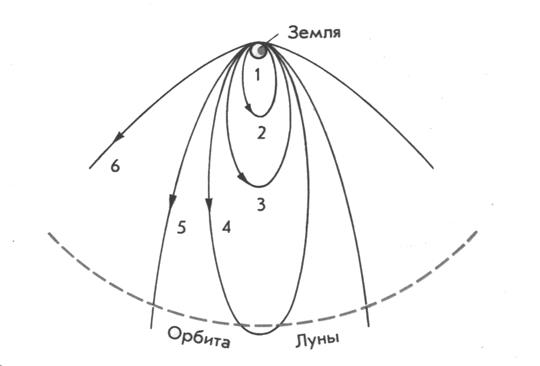Зависимость формы орбиты искусственного небесного тела от начальной
скорости 
. Орбиты при различных
начальных скоростях (векторы скоростей во всех случаях направлены горизонтально,
т. е. перпендикулярно, радиусу Земли):
Рис. 3.
1—круговая (
); 2,3,4 — эллиптические
(при соответственно равных
10,0 км/с; 11,0 км/с; 11,1 км/с); 5 — параболическая (
); 6 — гиперболическая (
).
В «Математических началах натуральный философии» Ньютона мы находим решение задачи о движении комет. Ньютон первый предложил способ вычисления элементов кометных орбит по трем наблюдениям. При этом Ньютон предполагал, что кометы описывают очень вытянутые эллипсы, так что их орбиты можно принять параболическими без чувствительной погрешности.
В сотрудничестве со своим учеником Галлеем Ньютон применил свой способ определения параболических орбит к вычислению орбиты большой кометы 1680 г. Это вычисление, приведенное в «Началах», показало, что сравнение широт и долгот кометы, вычисленных теоретически, с наблюденными дает очень хорошее согласие. Таким образом, было твердо установлено, что кометы движутся по своим параболическим орбитам под действием силы солнечного притяжения так же, как планеты по своим орбитам.
Методические рекомендации:
Данное занятие можно провести не в форме лекции. Можно организовать «круглый стол». Дать задание ученикам найти интересные исторические сведения об эллипсе, параболе и гиперболе, их применения в науке, технике и архитектуре. И провести на уроке обсуждение материала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.