Для проведения урока закрепления знаний по всей главе необходимо просить учеников обобщить сведения касающиеся параболы, гиперболы и эллипса (определения, канонические уравнения, бескоординатные уравнения эксцентриситет, директрисы, фокальные свойства и т.д.) и занести все данные в таблицу.
|
Эллипс |
Гипербола |
Парабола |
|
|
Определение |
|||
|
График |
|||
|
Бескоординатное уравнение |
|||
|
Каноническое уравнение |
|||
|
Эксцентриситет |
|||
|
Директрисы |
|||
|
Фокальное свойство |
|||
|
Касательные |
На заключительном занятии можно обсудить с учащимися значение кривых второго порядка. (Несколько учащихся должны будут подготовить доклады о применении эллипса параболы и гиперболы в современном мире. Это может быть техника, архитектура, наука, искусство).
Для того чтобы еще раз показать значение алгебры в геометрии можно предложить учащимся для рассмотрения способ приведения общего уравнения второй степени к каноническому виду. Но тогда данной теме нужно будет посвятить отдельное занятие, на котором нужно будет не только повторить формулы сокращенного умножения и метод выделения полного квадрата, но и дать понятие кривых второго порядка отличных от параболы, гиперболы и эллипса.
2.4.4.1.Распознавание линий второго порядка по их уравнениям
Рассмотрим общее уравнение второго порядка:
![]() (*).
(*).
Часто приходится отвечать на вопрос: “Какая линия является графиком уравнения?”
Для того, чтобы избавится от члена ![]() необходимо производить поворот системы координат, это под силу студенту,
но не каждый ученик с этим справиться, поэтому, для школьников предлается
рассматривать уравнения линий в которых уже нет члена содержащего произведение
координат.
необходимо производить поворот системы координат, это под силу студенту,
но не каждый ученик с этим справиться, поэтому, для школьников предлается
рассматривать уравнения линий в которых уже нет члена содержащего произведение
координат.
Такое уравение имеет вид:
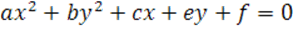
Для ответа на этот вопрос пользуются следующей схемой преобразования уравнения (*) – это выделение полного квадрата по одной или двум переменным.
Задания: Определить какая линия является графиком уравнения.
1. 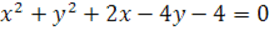
Решение:
Выделим полные квадраты.
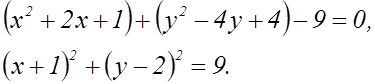
Следовательно, это окружность радиуса 3 с центром в
точке ![]() .
.
Изображение:
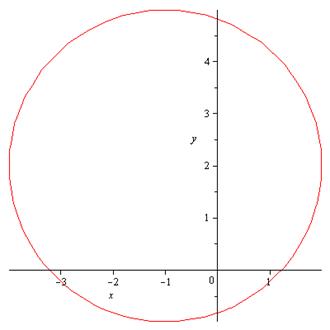
2.
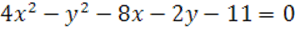
3. 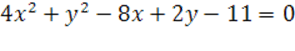
4.
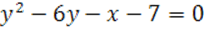
5.
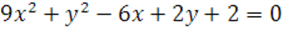
6. 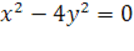
7. 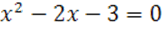
8. 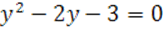
9. 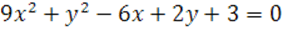
Также во время изучения данной главы, следует обратить внимание на понятие геометрическое место точек, и способу записи бескоординатных уравнений кривых, заданных определенными условиями. Это позволит включить в развитие пространственное мышление.
Приложение 1.
Привести уравнение квадрики к каноническому виду, определить её вид
1. ![]() в
в ![]()
Решение:
В наших обозначениях имеем
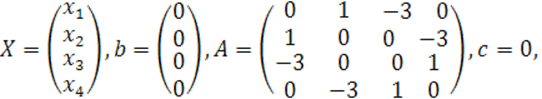
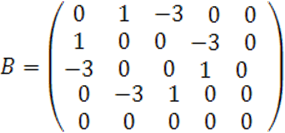
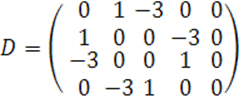
Ранги матриц ![]() определим методом окаймления.
определим методом окаймления.
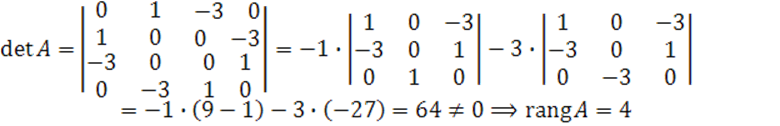
В матрице ![]() возьмем первые четыре столбца и посчитаем определитель:
возьмем первые четыре столбца и посчитаем определитель:
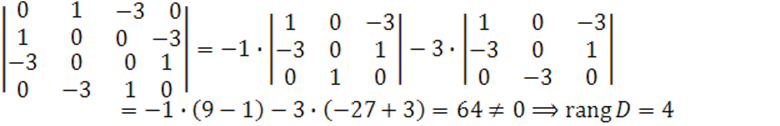
Получили ![]() квадрика центральная
квадрика центральная![]() каноническое уравнение имеет вид
каноническое уравнение имеет вид
![]()
где ![]()
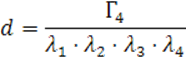
Решим уравнение
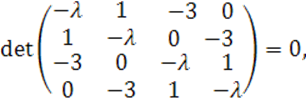
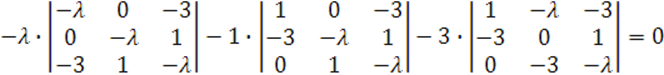
![]()
![]()
![]()
![]()
Посчитаем ![]()
![]() (так как матрица
(так как матрица ![]() содержит нулевую строку)
содержит нулевую строку)
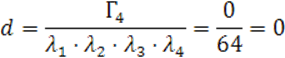
Запишем каноническое уравнение квадрики:
![]()
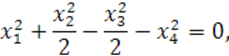
Это уравнение конуса индекса 2. Задача решена.
2.
![]() в
в ![]()
Решение:
В наших обозначениях имеем
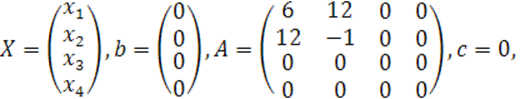
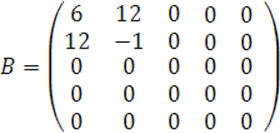
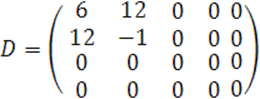
Ранги матриц ![]() определим методом окаймления.
определим методом окаймления.
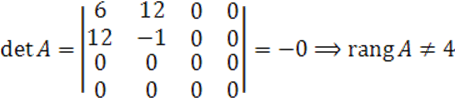
![]() (так как определителей большей размерности и отличных от нуля нет)
(так как определителей большей размерности и отличных от нуля нет)
![]()
Получили ![]() квадрика не центральная
квадрика не центральная![]() каноническое уравнение имеет вид
каноническое уравнение имеет вид
![]()
где ![]()
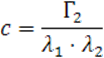
Решим уравнение
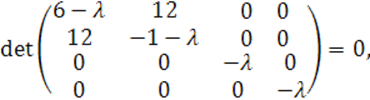
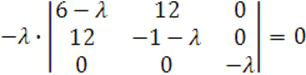
![]()
![]()
![]()
Посчитаем ![]()
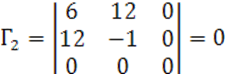
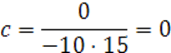
Запишем каноническое уравнение квадрики:
![]()
Это уравнение конуса c 2-мерной вершиной. Задача решена.
3.
![]() в
в ![]()
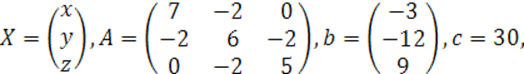
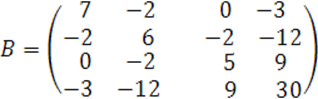
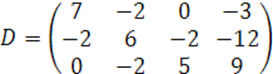
Ранги матриц ![]() определим методом окаймления.
определим методом окаймления.
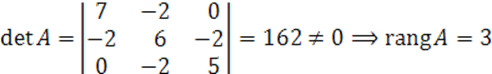
![]()
Получили ![]() квадрика центральная
квадрика центральная![]() каноническое уравнение имеет вид
каноническое уравнение имеет вид
![]()
где ![]()
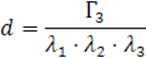
Решим уравнение
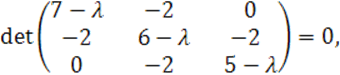
![]()
![]()
Посчитаем ![]()
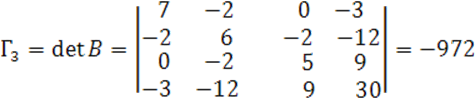
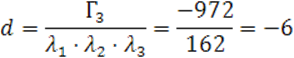
Запишем каноническое уравнение квадрики:
![]()
![]()
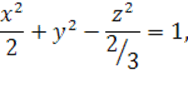
Это уравнение эллипсоида. Задача решена.
4.
![]()
в ![]()
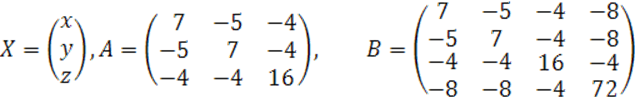
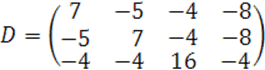
Ранги матриц ![]() определим методом окаймления.
определим методом окаймления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.