3. Из уравнения (3) следует, что уменьшаемое ![]() не
меньше
единицы,
т. е. что
не
меньше
единицы,
т. е. что 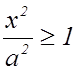 или
или ![]() . Это означает, что точки гиперболы
расположены справа от прямой
. Это означает, что точки гиперболы
расположены справа от прямой ![]() (правая ветвь гиперболы) и слева от прямой
(правая ветвь гиперболы) и слева от прямой ![]() (левая ветвь гиперболы).
(левая ветвь гиперболы).
4. Из уравнения (3) гиперболы видно, что когда ![]() возрастает, то и
возрастает, то и ![]() возрастает. Это
следует из того, что разность
возрастает. Это
следует из того, что разность 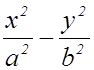 сохраняет
постоянное значение, равное единице.
сохраняет
постоянное значение, равное единице.
Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 16 (кривая, состоящая из двух неограниченных ветвей).
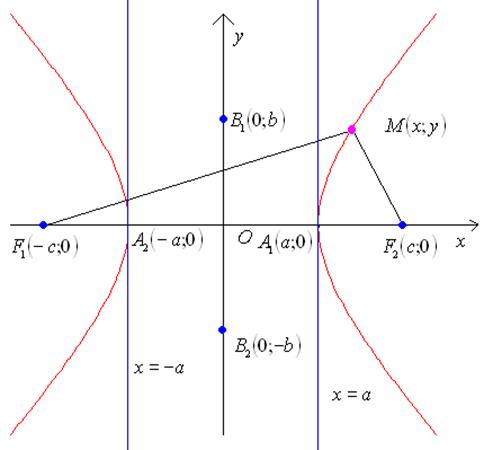
Рис. 16. Гипербола
Определение: Прямая ![]() называется асимптотой неограниченной
кривой
называется асимптотой неограниченной
кривой ![]() , если расстояние
, если расстояние ![]() от точки
от точки ![]() кривой
кривой ![]() до этой прямой стремится к нулю при
неограниченном удалении точки
до этой прямой стремится к нулю при
неограниченном удалении точки ![]() вдоль кривой
вдоль кривой ![]() от начала координат.
от начала координат.
Гипербола 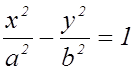 имеет две асимптоты:
имеет две асимптоты:
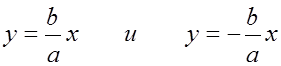 . (Рис. 17)
. (Рис. 17)
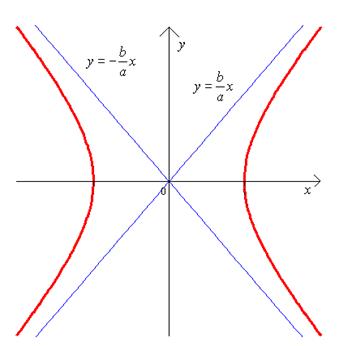
Рис.17. Гипербола с ассимпотами
При построении гиперболы целесообразно
сначала построить основной прямоугольник гиперболы (см. рис. 18), провести прямые,
проходящие через противоположные вершины этого прямоугольника, — асимптоты гиперболы
и отметить вершины ![]() и
и ![]() гиперболы.
гиперболы.
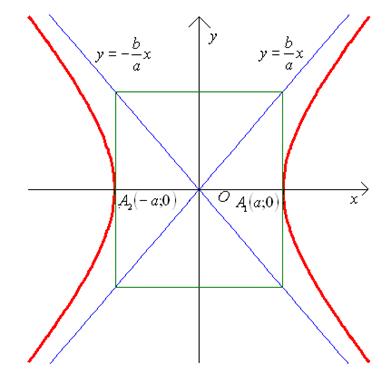
Рис. 18.
Определение: Гипербола называется равносторонней, если ее
полуоси равны (![]() ). Ее каноническое уравнение
). Ее каноническое уравнение
![]()
Асимптоты равносторонней гиперболы имеют
уравнения ![]() и
и ![]() и, следовательно, являются
биссектрисами координатных углов.
и, следовательно, являются
биссектрисами координатных углов.
( Рис. 19).
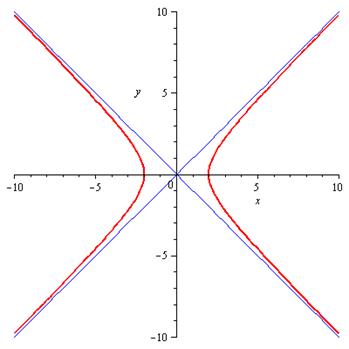
Рис. 19. Равносторонняя гипербола.
Уравнение равносторонней гиперболы, для которой
оси ![]() и
и ![]() являются
асимптотами, будет иметь знакомый нам вид
являются
асимптотами, будет иметь знакомый нам вид 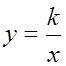 .
.
2.3.3. Дополнительные сведения о гиперболе
Определение: Эксцентриситетом гиперболы
называется отношение расстояния между фокусами к величине
действительной оси гиперболы, обозначается ![]() :
:
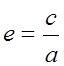 .
.
Так как для гиперболы ![]() , то эксцентриситет гиперболы больше
единицы:
, то эксцентриситет гиперболы больше
единицы: ![]() . Эксцентриситет
характеризует форму гиперболы.
. Эксцентриситет
характеризует форму гиперболы.
Действительно, из равенства ![]() следует, что
следует, что 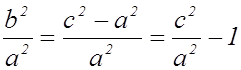 , т. е.
, т. е. 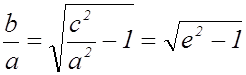 и
и 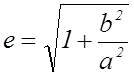 .
.
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение - ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет равносторонней гиперболы равен ![]() . Действительно,
. Действительно,
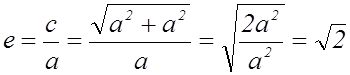
Фокальные радиусыдля точек правой ветви
гиперболы имеют вид ![]() и
и ![]() , а для левой
, а для левой ![]() и
и ![]() .
.
Определение: Прямые 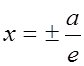 называются директрисами гиперболы.
Так как для гиперболы
называются директрисами гиперболы.
Так как для гиперболы ![]() , то
, то 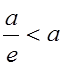 . Это значит, что правая директриса расположена между центром и правой вершиной гиперболы,
левая — между центром и левой вершиной.
. Это значит, что правая директриса расположена между центром и правой вершиной гиперболы,
левая — между центром и левой вершиной.
Директрисы гиперболы имеют то же свойство 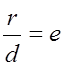 , что и директрисы эллипса. Кривая, определяемая
уравнением
, что и директрисы эллипса. Кривая, определяемая
уравнением 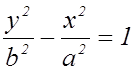 , также есть гипербола,
действительная ось которой
, также есть гипербола,
действительная ось которой ![]() расположена на оси
расположена на оси ![]() , а мнимая ось
, а мнимая ось ![]() — на оси
— на оси ![]() . На рисунке 20
она изображена пунктиром.
. На рисунке 20
она изображена пунктиром.
Гиперболы 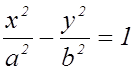 и
и 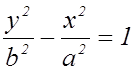 имеют общие асимптоты.
Такие гиперболы называются сопряженными.
имеют общие асимптоты.
Такие гиперболы называются сопряженными.
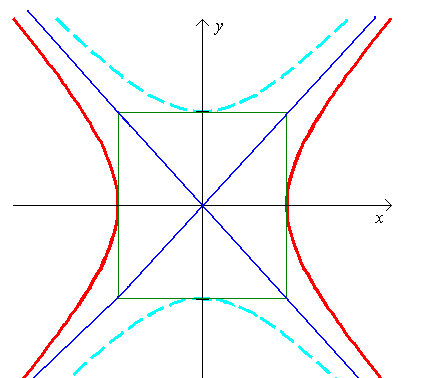
Рис. 20.
2.3.3.1. Касательные к гиперболе
Рассмотрим ветвь гиперболы, точки которой удовлетворяют равенству
![]() . Она разбивает плоскость
на две области — внешнюю, для точек
. Она разбивает плоскость
на две области — внешнюю, для точек
![]() которой
выполняется неравенство
которой
выполняется неравенство![]() , и внутреннюю,
для точек
, и внутреннюю,
для точек ![]() которой выполняется неравенство
которой выполняется неравенство
![]() .
.
Определение: Прямая, проходящая через точку ![]() гиперболы, называется касательной кгиперболе, если остальные точки этой прямой лежат во внешней области, то
есть удовлетворяют неравенству
гиперболы, называется касательной кгиперболе, если остальные точки этой прямой лежат во внешней области, то
есть удовлетворяют неравенству![]() . Точка
. Точка ![]() называется точкой касания.
называется точкой касания.
Аналогичным образом определяется касательная для точки, лежащей на другой ветви гиперболы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.