Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 8

Квадрику общего вида в - мерном пространстве можно рассматривать как сечение конуса (32) в  -мерном пространстве -мерной плоскостью, не проходящей через его вершину. В самомделе, уравнение (2) можно записать в виде (33)

                      (33)

где  — матрица -го порядка, следовательно, квадрику (2) можно рассматривать как пересечение конуса 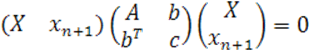 (34)

                               (34)

в -пространстве -мерной плоскостью.

Заметим, что  для квадрики (2) совпадает с определителем  для конуса (34), т.е. в том случае, когда конус (34) является центральной квадрикой, он высекает из плоскости  невырожденную квадрику (2).

1.6.3. Параболоиды

Рассмотрим теперь невырожденные нецентральные квадрики. Нецентральная квадрика может быть невырожденной только в том случае, когда , так как  определитель матрицы   не может быть отличен от нуля, если ранг матрицы  меньше . (Тогда в матрице  будет 2 пропорциональные строки, тогда определитель равен 0)

Поэтому в этом случае в уравнении (22) квадрики, приведенном к главным направлениям, отличны от нуля  из чисел  и уравнение (22) можно переписать в виде (35)

 (35)

Рассматривая уравнение (35) без слагаемого  , мы получаем уравнение центральной  квадрики в пространстве. Приводя уравнение этой квадрики к ее центру, мы преобразуем уравнение (35) к виду

Коэффициенты  не изменятся, так как при пепеносах матрица  является инвариантом.

Далее,  перенос

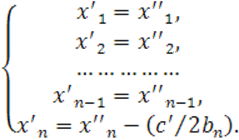
преобразует это уравнение к виду

                     

 (36)

Введем  обозначения

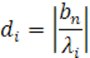
Тогда в случае, когда числа  имеют одинаковые знаки, уравнение (36) можно переписать в виде (37)

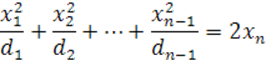
(37)

или привести к этому виду изменением направления -й координатной оси.

Поверхность (37) называется эллиптическим параболоидом (при  уравнение (37) является уравнением параболы, при  — уравнением эллиптического параболоида - х мерного пространства).

В случае, когда числа  при   имеют один знак, а при

—другой знак, уравнение (36) можно переписать в виде (38)

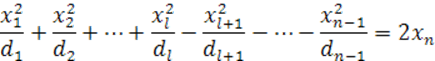
(38)

или привести к этому виду изменением направления -й координатной оси.

Поверхность (38) называется гиперболическим параболоидом индекса ;

всегда можно считать, что  , так как случай  приводится к этому случаю умножением всех членов уравнения на  и изменением направлений -й координатной оси (при и уравнение (38) является уравнением гиперболического параболоида - х мерного пространства).

Так  как  матрица  для параболоидов   (37)  и (38) имеет соответственно вид

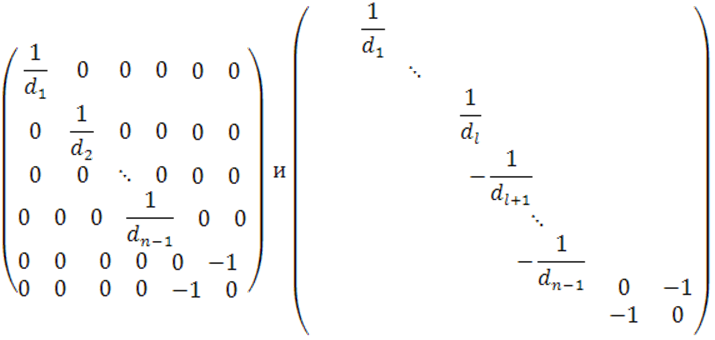
 этих матриц равны соответственно

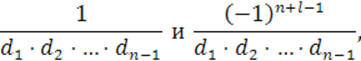
т. е. , и параболоиды действительно являются невырожденными квадриками.

1.6.4. Вырожденные квадрики

В общем случае вырожденная квадрика является нецентральной поверхностью и матрица ее оператора  имеет ранг . В этом случае в уравнении (22) квадрики, приведенном к главным направлениям, отличны от нуля чисел  и уравнение (22) можно переписать в виде (39)

(39)

Убирая из рассмотрения уравнения (39) слагаемые , мы получим уравнение центральной квадрики в пространстве. Приводя уравнение этой квадрики к ее центру, мы преобразуем уравнение (39) к виду (40)

(40)

Если хотя бы один из коэффициентов  отличен от нуля, перенос

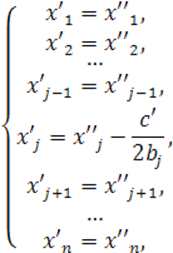
преобразует уравнение к виду (41)

.

(41)

Далее поворот в мерной плоскости  переводящий вектор с координатами   в вектор с координатами  переводит  уравнение (41) в уравнение (42)

(42)

Так как в уравнение (42) не входят координаты   это уравнение является уравнением цилиндра; так как уравнение (42) является уравнением параболоида в плоскости , то поверхность (42) называется параболическим цилиндром с мерным основанием или, короче, с основанием; в случае, когда параболоид в

плоскости эллиптический, будем называть цилиндр параболическим цилиндром индекса 0, в случае, когда параболоид в плоскости — гиперболический индекса , будем называть цилиндр параболическим цилиндром индекса (при  уравнение (42) является уравнением параболического цилиндра х мерного пространства).

В случае, когда в уравнении (40) все коэффициенты  равны нулю, это уравнение принимает вид (43)

.

(43)