Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 20

2.4. Парабола

2.4.1. Основные сведения

Мы с вами ознакомились с двумя кривыми второго порядка, эксцентриситет которых был либо меньше 1(эллипс), либо больше  1 (гипербола). Пришла пора рассмотреть кривую эксцентриситет, которой равен 1 – это парабола.

Определение: Пусть на плоскости задана прямая и точка , не принадлежащая этой прямой. Геометрическое место точек, равноудаленных от прямой и точки , называется параболой. Прямая называется директрисой, а точка — фокусом параболы (рис. 25).

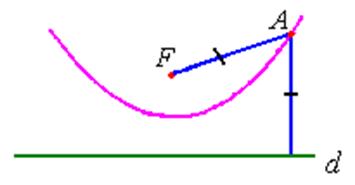
Рис. 25.

Для того чтобы нарисовать параболу, потребуются линейка, угольник, нить длиной, равной большему катету угольника, и кнопки. Прикрепим один конец нити к фокусу, а другой — к вершине меньшего угла угольника. Приложим линейку к директрисе и поставим на нее угольник меньшим катетом. Карандашом натянем нить так, чтобы его острие касалось бумаги и прижималось к большему катету. Будем перемещать угольник и прижимать к его катету карандаш так, чтобы нить осталась натянутой. При этом карандаш будет вычерчивать на бумаге параболу (рис. 26).

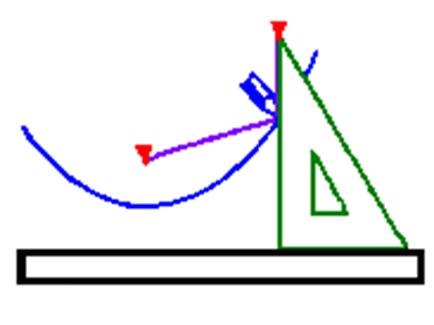
Рис. 26.

Свойства параболы

. Парабола симметрична относительно прямой проходящей через фокус перпендикулярно директрисе.

Доказательство. Пусть точка лежит на параболе, а  ей симметричная относительно прямой . (рис.27.)

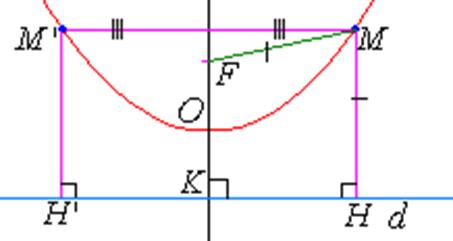
Рис. 27.

1. , так как отрезок   симметричен отрезку  относительно прямой .

2. , так как отрезок   симметричен отрезку  относительно прямой .

3. , так как  лежит на параболе.

4. Получаем, , следовательно, точка лежит на параболе.

. Середина отрезка  лежит на параболе.

По определению параболы  .

Определение: Осью параболы называется прямая, проходящая через фокус и перпендикулярная директрисе. Точка пересечения параболы с ее осью называется вершиной параболы.           

Определение: Расстояние от фокуса до директрисы называется параметром параболы, и обозначается .

Для вывода уравнения параболы выберем систему координат  так, чтобы ось  проходила через фокус  перпендикулярно директрисе в направлении от директрисы к , а начало координат  расположим посередине между фокусом и директрисой. Для того чтобы определить параболу достаточно знать её параметр .

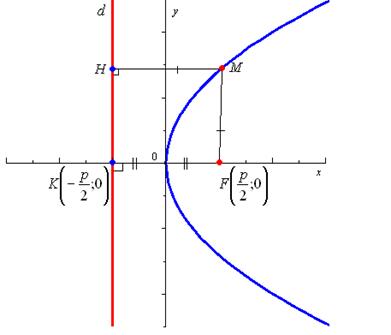
Рис. 28.

Расстояние между точками  и  равно параметру  . Пусть наша парабола проходит через начало координат. Из свойства  нам известно что  .

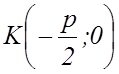Следовательно, точки  и имеют следующие  координаты:  и .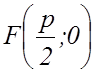

Возьмем произвольную точку  , лежащую на параболе.

Тогда . (*)

Точка  имеет координаты .

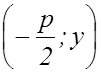Запишем условие (*) в координатах:

;

;

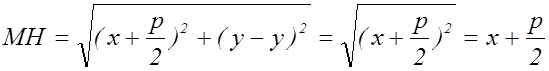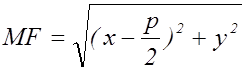Тогда, имеем 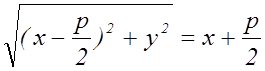. Возведем обе части в квадрат.

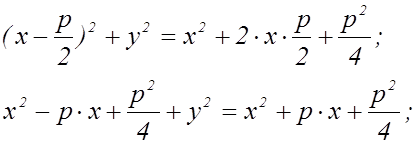
Приведем подобные члены:

Получили каноническое уравнение параболы.

Также будем считать каноническими следующие уравнения:

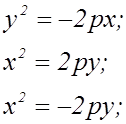
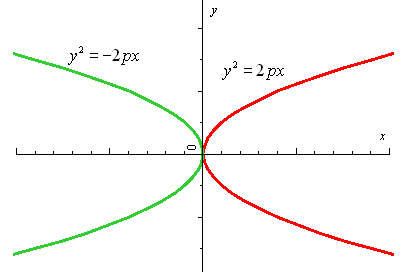
Рис. 29.

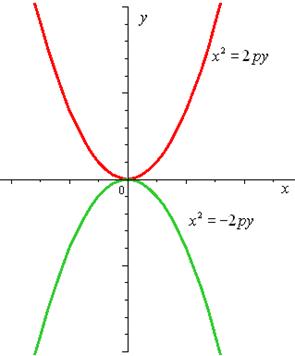
Рис. 30.

Определение: отрезок называется фокальным радиусом точки .

Пример. Найти расстояние от вершины до фокуса параболы заданной уравнением

Решение:

Одно из канонических уравнений имеет вид: . Запишем данное уравнение в каноническом виде: 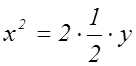. Следовательно 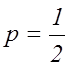. А значит расстояние от фокуса до вершины равно . (см. рис.28).

Определение: Прямая, имеющая с параболой только одну общую точку и не перпендикулярная ее директрисе, называется касательной к параболе.

Теорема 1. Пусть — точка на параболе с фокусом и директрисой , — перпендикуляр, опущенный на директрису (рис. 31). Тогда касательной к параболе, проходящей через точку , будет прямая, содержащая биссектрису угла .

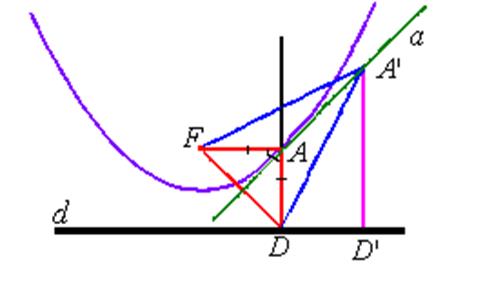
Рис.31.

Доказательство. Докажем, что прямая , содержащая биссектрису угла , будет касательной к параболе (рис. 31). Действительно, треугольник — равнобедренный, так как по определению параболы . Следовательно, прямая  будет серединным перпендикуляром к отрезку . Для произвольной точки прямой  отличной от , опустим перпендикуляр на прямую . Тогда , так как прямая - серединным перпендикуляром к отрезку . , так как  - наклонная к прямой , а - перпендикуляр. Следовательно , а это означает, что точка не принадлежит параболе, следовательно, прямая имеет только одну общую точку  с параболой, то есть является касательной.