Основные инварианты,позволяющие однозначно определить вид и каноническую запись квадрики, страница 9

Так как в уравнение (43) не входят координаты , это уравнение также является уравнением цилиндра. В случае, когда , и уравнение (43) является уравнением эллипсоида в плоскости

, поверхность (43) называется эллиптическим цилиндром с основанием в случае, когда уравнение (43) является уравнением гиперболоида в той же плоскости, поверхность (43) называется гиперболическим цилиндром с основанием, причем в случае, когда гиперболоид в плоскости — гиперболоид индекса , цилиндр называется гиперболическим цилиндром индекса , в случае, когда уравнение (43) является уравнением мнимого эллипсоида в той же плоскости, уравнение (43) называется уравнением мнимого цилиндра с основанием (при  и  уравнение (43) в первых двух случаях является уравнением эллиптического и гиперболического цилиндров х мерном пространства).

При  и уравнение (43) принимает вид

что можно переписать     в виде (44)

(44)

а при — в виде (45)

(45)

Уравнение (44) является совместным уравнением пары параллельных плоскостей , уравнение (45) по аналогии называется уравнением пары мнимых параллельных плоскостей .

В случае, когда , и уравнение (43) является уравнением мнимого конуса в плоскости , этому уравнению удовлетворяют только точки  плоскости . В случае, когда , и уравнение (43) является уравнением конуса в той же плоскости, поверхность (43) называют конусом с мерной вершиной или, короче, с вершиной; в предыдущем случае это уравнение по аналогии с этим случаем называют уравнением мнимого конуса с

вершиной; конус называется конусом индекса , если  (случай, когда , приводится к этому случаю умножением всех членов уравнения на ). При , когда вершиной конуса является точка, будем называть конус конусом с точечной вершиной.

При  и уравнение (43) принимает вид (46)

(46)

т. е. в первом случае его можно переписать в виде (47)

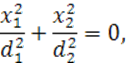
(47)

а во втором случае — в виде (48)

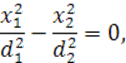
(48)

Уравнение   (48)  является   совместным   уравнением пары пересекающихся плоскостей (49)

(49)

уравнение (47) по аналогии называется уравнением пары мнимых пересекающихся плоскостей (50)

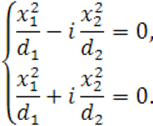
(50)

При  и уравнение (43) принимает вид (51)

(51)

т. е. является уравнением пары слившихся плоскостей. Роль плоской вершины при играет плоскость пересечения плоскостей (в случае пар плоскостей (47) и (48) — плоскость ), при

— плоскость, совпадающая со сливающимися плоскостями (в случае пары плоскостей (51) — плоскость ).

1.6.5. Исследование уравнений квадрик при помощи

метрических инвариантов

Так как движение общего вида  состоит из вращения и переноса, инвариантами уравнения квадрики при произвольных движениях являются те функции коэффициентов, которые являются инвариантами и при вращениях и при переносах. Такими инвариантами являются инвариант  и инварианты являющиеся функциями коэффициентов . Поэтому инварианты составляют полную систему  независимых инвариантов уравнения квадрики при произвольных движениях.

Вычислим метрические инварианты для различных типов квадрик (см. табл.).

Будем использовать ранее введенные обозначения.

Каноническая запись
	…………………………..
	………………………….
	………………………….
……………………………………..	…………………………..	………………
	…………………………
…………………………………….	…………………………….	………………