1.1.1. Общая задача линейного программирования формулируется следующим образом: найти экстремум целевой функции
Z (Х) = c1x1 + c2x2 + … + cnxn ® max (min), (1)
при ограничениях аi1х1 + аi2х2 + … + аinхn = bi , i = 1, …, m1; (2)
аi1х1 + аi2х2 + … + аinхn ≤ bi , i = m1+1, …, m2; (3)
аi1х1 + аi2х2 + … + аinхn ≥ bi , i = m2 +1, …, m; (4)
х1 ³ 0, х2 ³ 0, . . . , хt ³ 0, t £ n . (5)
1.1.2. Основная задача линейного программирования
Z (Х) = c1x1 + c2x2 + … + cnxn ® max (min), (6)
при ограничениях аi1х1 + аi2х2 + … + ainxn = bi , i = 1, …, m; (7)
х1 ³ 0, х2 ³ 0, . . . , хn ³ 0. (8)
1.1.3. Правило приведения общей задачи ЛП к основной.
1) Если хk не подчинено условию неотрицательности, заменяем разностью хk = х′k - х′′k , х′k ³ 0 , х′′k ³ 0 .
2) Введем положительную дополнительную переменную в левую часть каждого из неравенств (3) со знаком "+", чтобы превратилось в равенство.
3) Введем положительную дополнительную переменную в левую часть каждого из неравенств (4) со знаком "-" , чтобы превратилось в равенство.
4) В целевую функцию дополнительные положительные переменные вводятся с коэффициентом, равным нулю.
Пример 1. Привести к основному виду задачу ЛП Z(Х) = 3x1 + x2 + x3 → max (min),
x1 + 2x2 + x3 = 7,
x1 - x2 + 2x3 ≤ 1,
2x1 + x2 + 2x3 ≥ 5,
x2 ≥ 0, x3 ≥ 0.
Решение. 1) х1 не подчинено условию неотрицательности, заменяем разностью х1 = х1′ - х1′′, х1′ ≥ 0, х1′′ ≥ 0.
2) Введем х4 ≥ 0 в левую часть неравенства х1 – х2 + 2х3 ≤ 1 со знаком «+», чтобы превратилось в равенство х1 – х2 + 2х3 + х4 =1, где х4 = 1 – х1 + х2 – 2х3.
3) Введем х5 ≥ 0 в левую часть неравенства 2x1 + x2 + 2x3 ≥ 5 со знаком «-», чтобы оно превратилось в равенство 2х1 +x2 +2x3 –х5 =5, где х5= -5+2х1+х2+2х3.
4) В целевую функцию х4, х5 вводятся с коэффициентом, равным нулю.5)Запишем задачу в основном виде:
Z (Х) = 3х1′ - 3х1′′ + x2 + x3 + 0 х4 + 0х5 → mах (min), (9)
х1′ - х1′′ + 2х2 + х3 = 7, х1′ - х1′′ - х2 + 2х3 + х4 = 1, (10)
2х1′- 2х1′′ + х2 + 2х3 - х5 =5, х1′ ≥ 0, х1′′ ≥ 0, х2 ≥ 0, х3 ≥ 0, х4 ≥ 0, х5 ≥ 0. (11)
1.2. Симплекс-метод .Пусть поставлена задача ЛП. Найти минимум (максимум) функции
Z(Х) = c1x1 + c2x2 + … + cnxn, (1)
при ограничениях:
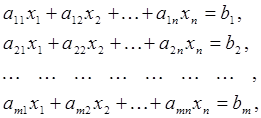 (2)
(2)
хi ³ 0, i = 1, 2, …, n, (3)
bj ³ 0, j = 1, 2, …, m, m<n. (4)
Перепишем эту задачу в векторной форме:
Найти минимум (максимум) функции Z(Х) = c1x1 + c2x2 + … + cnxn, при ограничениях
![]()
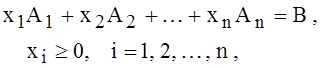 (5)
(5)
где
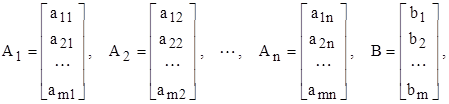
m – Мерные вектор-столбцы.
1.2.1 Определения. 1º. Любые m переменных системы (2) называются базисными (или основными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n-m переменных называются небазисными.
2º. Решение Х0 = (х1, х2, …, хn) системы (2) называется:
а – планом или допустимым, если xi ≥ 0 для любых i = 1, 2, …, n;
б – базисным, если n-m небазисных переменных равны нулю, т.е. Х0 = (х1, х2, …, xm, 0, …, 0);
в – вырожденным, если Х0 - базисное решение и хотя бы одна из базисных переменных равна нулю.
г – опорным, если X0 – базисное решение и векторы А1, А2, …, Аm, входящие в разложение (5) с положительными коэффициентами хj, являются линейно-независимыми.
3º. Оптимальным решением (планом) задачи ЛП (1) – (4) называется решение, доставляющее наименьшее (наибольшее) значение линейной функции Z(X).
Пусть требуется найти минимальное (максимальное) значение функции
Z(Х) = c1x1 + с2x2 +…+ cnxn при ограничениях:
1х1 + 0х2 + … + 0хm + a1 m+1xm+1 + … + a1nxn = b1 ,
0х1 + 1х2 + … + 0хm + a2 m+1xm+1 + … + a2nxn = b2 ,
. . . . . . . . . . . . . . . . . . (6)
0х1 + 0х2 + … + 1хm + am m+1xm+1 + … + amnxn = bm ,
xi ³ 0 , i = 1, 2 ,…, n , bj ≥ 0 , j = 1, 2, …, m.
Заметим теперь, что система (6) имеет матрицу
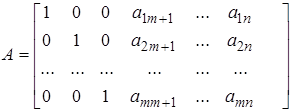 .
.
Векторная форма данной задачи имеет следующий вид: Найти минимум (максимум) функции
Z(Х) = c1x1 + с2x2 +…+ cnxn , при ограничениях
![]()
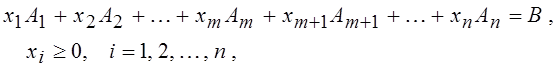
где 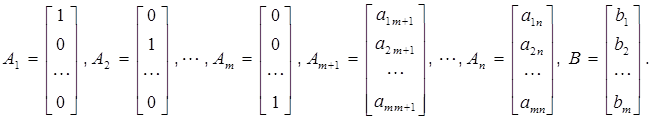
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.