Задача линейного программирования. Проверка оптимальности текущего плана, страница 22

Пример 1. Для транспортной задачи, исходные данные которой приведены в таблице 2, требуется:

Таблица 2

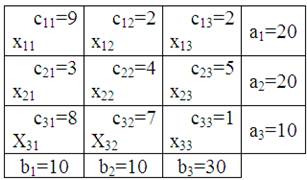
1) составить математическую модель ТЗ; 2) составить первоначальный план методом:- северо-западного угла, минимального элемента ; 3) найти оптимальный план методом потенциалов.

Решение. Составление математической модели ТЗ

Матрица перевозок                       Матрица стоимостей

,                      

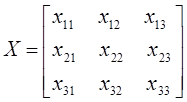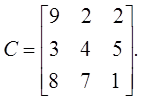
Математическая модель задачи состоит в нахождении переменных задачи, обеспечивающих минимум функции  Z (Х) =9х₁₁ +2х₁₂ +2х₁₃ + 3х₂₁ + 4х₂₂ + 5х₂₃ + 8х₃₁ + 7х₃₂ + 1х₃₃

и удовлетворяющих системе ограничений х₁₁ + х₁₂ + х₁₃ = а₁ = 20, х₂₁ + х₂₂ + х₂₃ = а₂ = 20, х₃₁ + х₃₂ + х₃₃ = а₃ = 10, х₁₁ + х₂₁ + х₃₁ = b₁ = 10, х₁₂ + х₂₂ + х₃₂ = b₂ = 10, х₁₃ + х₂₃ + х₃₃ = b₃ = 30, х_ij ≥ 0,   i = 1, 2, 3;  j = 1, 2, 3.

Так как 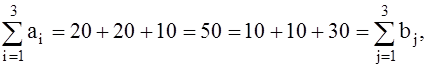 то задача закрытая.

Составление первоначального плана (Метод северо-западного угла)

Заполнение клеток табл. 2, начинается с левой верхней клетки (северо-западная часть таблицы) и продолжается вниз и вправо (по диагонали).

Таблица 3

1) В клетку (1, 1) занесем меньшее из чисел а₁=20 и b₁=10, т.е. 

2) Закроем первый столбец (где нет остатка).

3) Вычислим остатки первой строки.  .

4) Переходим к клетке (1, 2) и находим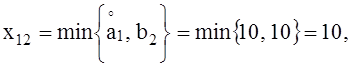в этом случае выберем один из двух вариантов: - положим х₁₂=10, х₂₂ = 0^* и закроем первую строку и второй столбец;- положим х₁₂=10, х₁₃ = 0^* и закроем второй столбец и первую строку.

Положим, например, х₁₂=10, х₂₂ = 0^* (таблица 3).

5) Переходим к клетке (2, 3):        

6) Закроем вторую строку.

7) Вычислим остатки третьего столбца     (табл. 4).

Таблица 4

8) Заполняем последнюю клетку (3, 3)

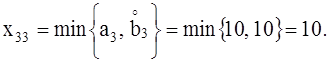
9) Проверяем правильность построения первоначального решения.

Число занятых клеток должно быть равно m + n – 1 = 3 + 3 – 1 = 5  (m – количество строк, n - количество столбцов). В табл. 4 занято 5 клеток.

10) Первоначальный план методом северо-западного угла равен

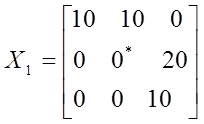.                                                                     (7)

11) Находим первоначальную стоимость на перевозку (см. табл. 4).

Z (Х₁) = 9∙10 + 2∙10 + 4∙ 0^* + 5∙20 + 1∙10 = 220.

(Метод минимального элемента). Заполнение клеток табл. 2 начинается с любой клетки, где стоит минимальный элемент.

1)Так как клетка (3, 3) табл. 2 имеет минимальный элемент, то заполняем её по формуле  х₃₃ =

2) Закроем третью строку (где нет остатка).

3) Вычислим остатки третьего столбца =b₃ – х₃₃ = 30 – 10 = 20 (табл. 5).

4) В оставшейся табл. 5 находим клетки с минимальным элементом. Таких клеток две – (1, 2) и (1, 3) со стоимостями перевозки равными 2. Сравним максимально возможные значения для этих клеток:

Для клетки (1, 2)  х₁₂ =

Для клетки (1, 3)  х₁₃ =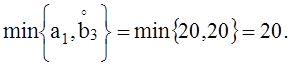

Так как  – то в клетку (1, 3), даем значение равное 20 единицам. Для заполнения клетки (1, 3) выбираем один из двух вариантов:

-положим х₁₃ = 20 , х₁₂ = 0^* и закроем первую строку и третий столбец;

-положим х₁₃ = 20 , х₂₃ = 0^* и закроем третий столбец и первую строку.