Задача линейного программирования. Проверка оптимальности текущего плана, страница 24

θ₂= {x₁₁=10, x₂₃=20} =10.

16) Вычитаем 10 в тех клетках, что помечены «-», и прибавляем 10 в тех клетках, что помечены «+». Получаем новый план.

Таблица 11                       Таблица 12

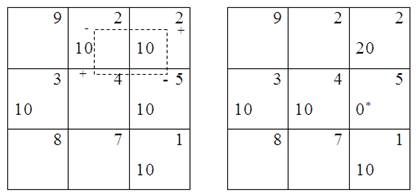
17) Снова проверяем оптимальность нового плана:

U₁+V₂= с₁₂=2, U₁+V₃= с₁₃=2, U₂+V₁= с₂₁=3, U₂+V₃= с₂₃=5, U₃+V₃= с₃₃=1.

Положим U₁=0, находим V₂=2; V₃=2; U₂=3; V₁=0; U₃=-1.

∆₁₁= U₁+V₁-с₁₁=0+0-9=-9<0, ∆₂₂= U₂+V₂-с₂₂=3+2-4=1>0,∆₃₁= U₃+V₁-с₃₁=-1+0-8=-9<0,

∆₃₂= U₃+V₂-с₃₂=-1+2-7=-6<0.Положительная единственная оценка – это ∆₂₂=1.

18) Находим в таблице 11 цикл:  (2,2)→(2,3)→(1,3)→(1,2)→(2,2)

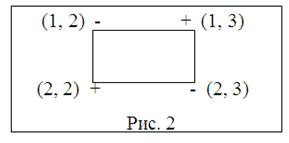
19) Находим θ₃= {x₁₂=10, x₂₃=10}=10.          

20) Вычитаем 10 в клетках (1,2), (2,3) и прибавляем в клетках (1,3), (2,2). Получаем новый план.

Нетрудно проверить оптимальность текущего плана и убедиться что все оценки свободных клеток отрицательные. При данном плане стоимость перевозок:

Z (Х) =2·20+3·10+4·10+1·10=120.

Второй способ

1) Положим, потенциал первой строки равен, например, нулю (U₁=0). Рядом с потенциалом в скобках записываем номер шага, т.е. рядом с U₁=0 запишем (1) (табл. 13).

2) Переходим к первой занятой клетке первой строки (1, 1) и находим потенциал первого столбца по формуле V₁ = c₁₁ – U₁ = 9 – 0 = 9 (шаг (2)).

3) Поскольку в первом столбце нет занятой клетки кроме (1, 1), поэтому переходим к следующей занятой клетке первой строки (1, 2) и находим потенциал второго столбца по формуле V₂ = c₁₂ – U₁ = 2 – 0 = 2 (шаг (3)).

4) Теперь известно V₂ = 2. Переходим к следующей занятой клетке второго столбца (2, 2) и находим потенциал второй строки  U₂= с₂₂ – V₂ = = 4 – 2 = 2   (шаг (4)).

5) Поскольку известен потенциал второй строки U₂ = 2, поэтому переходим к следующей занятой клетке этой строки (2,3) и находим потенциал третьего столбца  V₃= с₂₃ –U₂ =5 –2 =3(шаг (5)).

6) Известен потенциал V₃ = 3.Переходим к занятой клетке третьего столбца

(3, 3) и находим потенциал третьей строки U₃ = с₃₃ – V₃ =   1 – 3 = – 2 (шаг (6)).

Таким образом, мы подбирали потенциалы так, чтобы оценки заполненных клеток стали равными нулю Δ_ij = U_i + V_j – - с_ij = 0 (см. табл. 13).

7)  Находим оценки свободных клеток по формуле  Δ_ij= U_i + V_j – C_ij ≤ 0 (см. табл. 13).

8) Запишем оценки клеток таблицы 13 в виде отдельной матрицы.

9)Проверим оптимальность текущего плана по значениям оценок свободных клеток.

Если для всех свободных клеток (Δ_ij £ 0), то текущий план оптимален. Если хотя бы одна из оценок положительна (Δ_ij > 0), то план можно улучшить. Так как Δ₁₃ = 1,  Δ₂₁ = 8, то.

Таблица 13

10) Находим .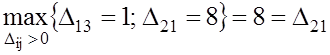

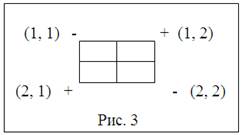
11) Для клетки (2, 1) ставим знак «+» и строим цикл (см.рис.3) .Следуя этому циклу, расставим чередующиеся знаки «+» и «-» в его вершинах, начиная с того знака «+», что уже стоит в вершине (2, 1).

12) Находим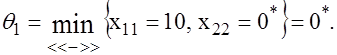          

13) Вычитаем число θ₁ = 0^* в клетках (1, 1), (2, 2) и прибавляем его в клетках (1, 2), (2, 1). Получаем новый план.

Таблица 14

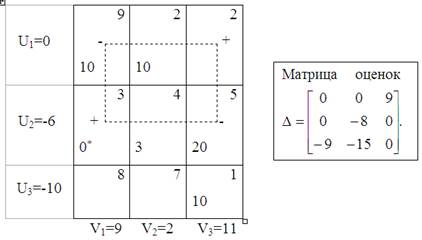
(Решение предлагается продолжить читателю самостоятельно).

6.1.5. Решение открытой транспортной задачи .Для открытой ТЗ может быть два случая:

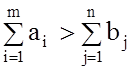1º. ; 2º. 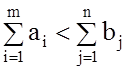. Открытая ТЗ решается сведением ее к закрытой ТЗ. В случае (1º), когда суммарные запасы превышают суммарной потребности, вводится фиктивный  потребитель со спросом 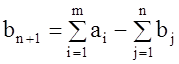.В случае (2º), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик с запасами .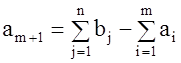

Стоимость перевозки единицы груза, как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится, т. е.  c_i(n+1) = 0 i, c_(m+1)j= 0 j.

Пример2.Решить транспортную задачу, исходные данные которой таковы:

Таблица 15