Задача линейного программирования. Проверка оптимальности текущего плана, страница 21

2. В ячейку А2 вводим значение, увеличенной на 0,2.

Выделяем ячейки А1:А2 и затем способом «автозаполнение» заполняем диапазон А1:А16.

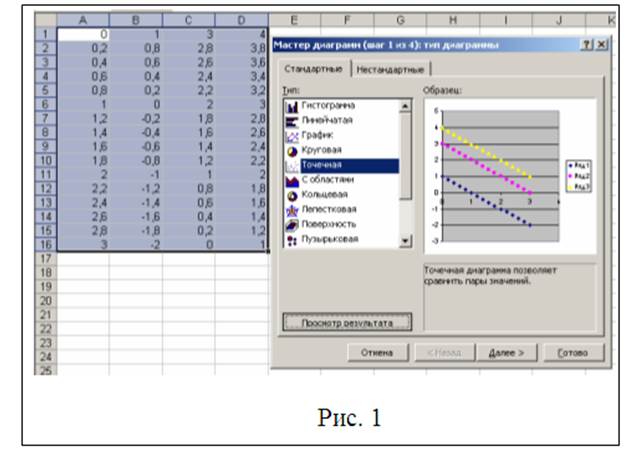
3. В ячейку В1 вводим формулу = 1 - А1.

Далее способом «автозаполне-ние» формируем диапазон В1:В16.

4.Вводим в ячейку С1 формулу = 3-А1. (Записали прямую х₁ + х₂ = 3). Затем также как в предыдущем случае заполняем диапазон С1:С16.

5.Вводим в ячейку D1 формулу = 4-А1. Затем также как в п.п. 2,3 заполняем диапазон D1:D16.

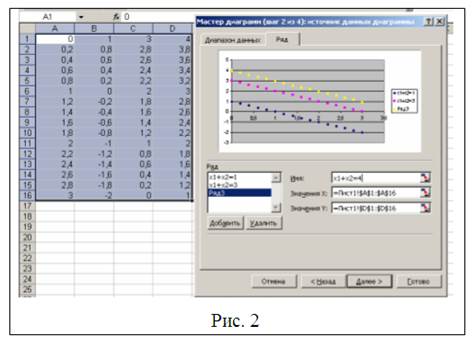
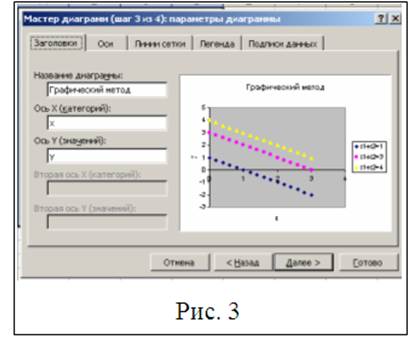
6.Выделяем диапазон ячеек А1:D16 и строим диаграмму с помощью команды Вставка→Диаграмма или с помощью соответствующей кнопки на панели инструментов программы Excel.  В диалоговом окне «Мастер диаграмм» выбираем точечный тип диаграммы.  Нажав на кнопку «Просмотр результата» и не отпуская ее, можно убедиться в правильности выбора типа диаграммы (рис.1). Нажав на кнопку «Далее» приходим ко второму диалоговому окну и в поле «Имя» вводим формулу х₁+х₂=1. Нажав кнопку «Добавить»  в тоже поле вводим формулу х₁+х₂=3 (рис. 2).Добавим еще одну формулу х₁+х₂=4 и получим результат представленный на рис. 2. На третьем шаге нужно убрать линии сетки с помощью вкладки «Сетка», на вкладке «Заголовки» в поле «Название диаграммы» введем Графический метод и выставим названия осей как представлено на рис. 3.

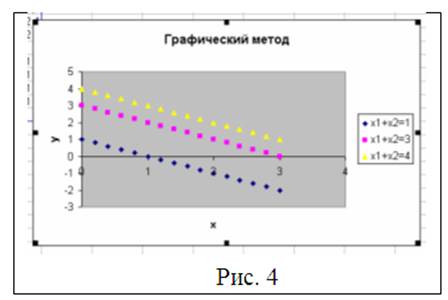
Перейдя к последнему шагу построения диаграммы, оставляем диаграмму на имеющемся листе и, нажав кнопку «Готово», получаем результат представленный на рис. 4.

Глава 3. транспортная задача

6.1.Транспортная задача по критерию стоимости перевозок. 6.1.1.Постановка задачи.

Однородный груз сосредоточен у m поставщиков в количествах  а₁, а₂, . . . ,а_m. Данный груз  необходимо доставить  n  потребителям в количествах b₁, b₂,  . . . , b_n. Известны С_ij (i = 1, 2, . . ., m;  j = 1, 2, . . ., n) – стоимости перевозки единицы груза от каждого i – го поставщика каждому j-му потребителю. Требуется найти план перевозок, при котором: 1) Запасы всех поставщиков вывозятся полностью. 2) Запросы всех потребителей удовлетворяются полностью.3) Суммарные затраты на перевозку всех грузов минимальны.

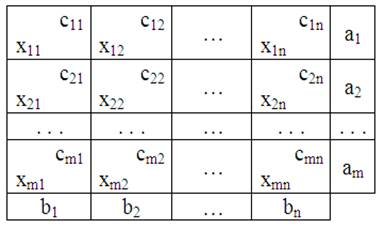
Решение. Обозначим через х_ij – количество единиц груза, перевозимого от каждого i-го поставщика каждому j-му потребителю. Исходные данные записываются в таблице вида:

Таблица 1

Математическая формулировка ТЗ состоит в следующем: Найти переменные задачи

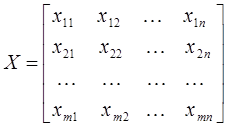,                                                                  (1)

удовлетворяющие системе ограничений х_i1 + x_i2 + … + x_in = a_i(i= 1, 2, …, m),                                              (2)

х_1j + x_2j + … + x_mj = b_j(j= 1, 2, …, n),                                               (3)

x_ij ≥ 0 (i = 1, 2, …, m; j = 1, 2, …, n)                                                (4)

и обеспечивающие минимум целевой функции Z (Х) = 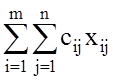.                                                                                                        (5)

6.1.2. Определения.1) Всякое неотрицательное решение систем линейных уравнений (2) и (3), определяемое матрицей(1), называется планом ТЗ. 2) План X^* =[x^*_ij] (i = 1, 2, …, m;  j =1, 2, …, n), при котором функция (4) принимает свое минимальное значение, называется оптимальным планом ТЗ.3)Если 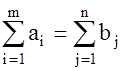, то ТЗ называется закрытой. 4)Если 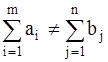, то ТЗ называется открытой.

6.1.3. Свойства транспортной задачи  ТЗ (2) – (5) имеет оптимальное решение

1).тогда и только тогда, когда 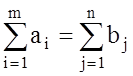,                                (6)

2).если в транспортной таблице 1 количество заполненных клеток равно m +n – 1 (m – число поставщиков, n – число потребителей).

6.1.4. Решение закрытой транспортной задачи. Для определения оптимального плана ТЗ начинают с нахождения какого-нибудь его первоначального плана. Для определения этого плана существует несколько методов. два из них – метод северо-западного угла, метод минимального элемент. Проверка на оптимальность этого плана ведётся методом потенциалов.