Задача линейного программирования. Проверка оптимальности текущего плана, страница 18

Придавая параметру t любые числовые значения от 0 до 1, получим различные оптимальные решения задачи, при любом из которых Z = Z_min = 24.

10. Перемещаем прямую Z=0, в направлении вектора.

Последней общей точкой с пятиугольником решений задачи является т. D.

11.Определяем координаты D=(L₃)Ç(L₄), решая систему

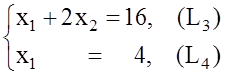
получим .

12. Вычисляем Z_max =Z(D)= 8∙4+4∙6 = 56. Таким образом, оптимальное решение  является единственным.

Пример 6. Найти минимум и максимум функции Z = 5x₁+5x₂  при условиях:

                                                                                     (1)

                                                                                     (2)

                                                                                             (3)

.                                                                                             (4)

Решение предлагается читателю выполнить самостоятельно и убедиться, что задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка [A, B]. min Z(X)=20, при

Общее решение: min Z(X)=20, при Х^* = (4-4t,4t),  0 ≤ t ≤ 1.

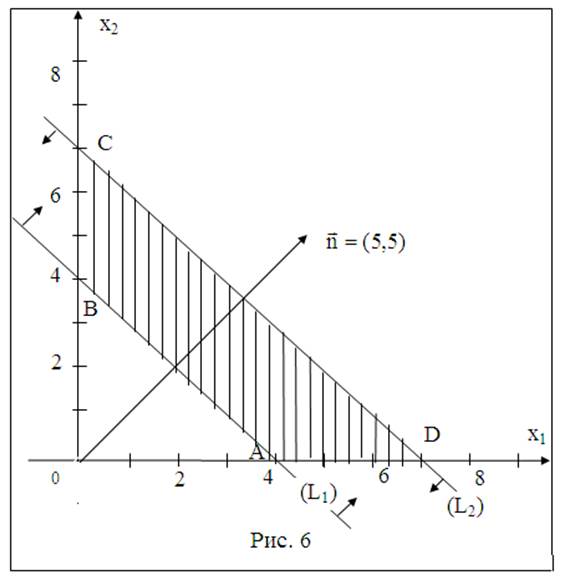
Аналогично убедиться в том, что задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка [С, D]. mах Z(X)=35, при

Общее решение: max Z(X)=35, при Х^* = (7t, 7-7t),  0 ≤ t ≤ 1.

Пример 7. Найти максимум и минимум функции Z=5(x₁+x₂)  при условиях:

                                                                                     (1)

                                                                                     (2)

                                                                                             (3)

.                                                                                             (4)

Решение.1.Согласно рис. 7 областью решений является отрезок АВ.

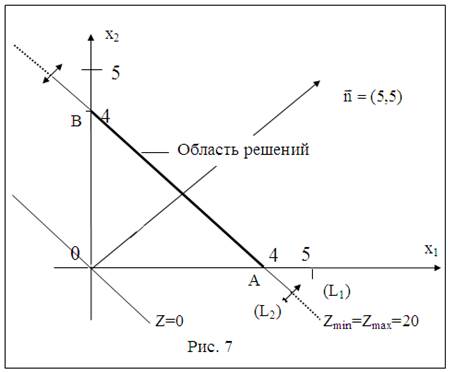
2.Строим прямую Z=0. Для этого строим вектор  и через т.О(0, 0) проводим прямую перпендикулярную ему.Перемещаем эту прямую в направлении вектора. Прямая Z совпадает с областью допустимых решений и проходит через две угловые точки этой области А и В.

3.Координаты точек А и В равны соответственно: .

4.Вычисляем Z(A)=Z(B)=Z_min=Z_max=20.

5.Задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка [A, B].          

min Z(x) = max Z(x) = 20.Общее решение: min Z(X) = max Z(X) = 20 при Х^* = (4-4t,4t), 0 ≤ t ≤ 1.

2.1.4. Отсутствие конечного оптимума (min Z(x) = -∞, max Z(x) = ∞)

Прямая Z сколько бы мы ее ни перемещали не занимает крайнего положения с областью допустимых решений.

Пример 8. Найти максимум и минимум функции Z=3x₁+5x₂ при условиях:

                                                                               (1)

                                                                                              (2)

                                                                                             (3)

.                                                                                             (4)

Решение.1.Строим область допустимых решений задачи.

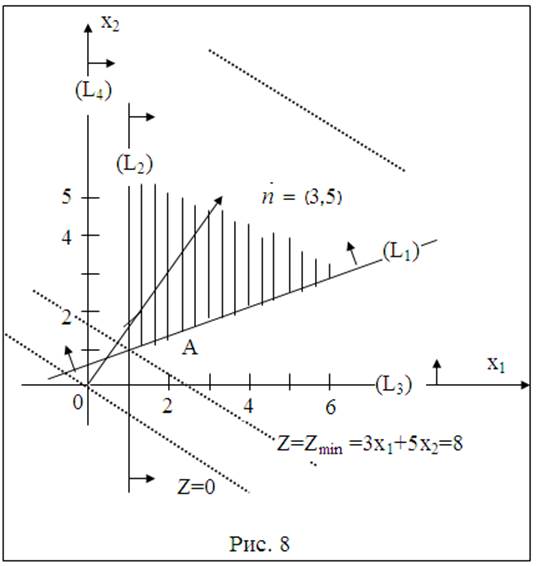
Для этого в неравенствах системы ограничений знаки неравенств заменяем на знаки точных равенств:

            (L₁),

                           (L₂),

                          (L₃),

                          (L₄).

Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение. Областью решений задачи является неограниченный многоугольник (см. рис. 8).

2.Строим прямую Z=0. Для этого строим вектор  и через т. О(0, 0) проводим прямую перпендикулярную ему. Передвигаем данную прямую в направлении вектора. Прямая Z встретит неограниченную многоугольную область в т. А и в ней Z(А)=Z_min. Перемещаем прямую Z в направлении возрастания, т.е. в направлении вектора. В виде того, что в этом направлении область допустимых решений не ограничена, прямая уходит в бесконечность. Задача не имеет решения вследствие неограниченности целевой функции, т.е. max Z(X) = +∞.