Задача линейного программирования. Проверка оптимальности текущего плана, страница 12

2) Составляем расширенную матрицу     .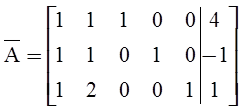

Так как элементы левой части второй строки положительны, а элемент правой части–отрицательный, то в этом случае задача не имеет решения.

°2) Если в строке с b_i < 0 имеется отрицательный элемент a_ij < 0 , то можно ввести в базис столбец ∆_j , в котором стоит этот элемент, с помощью допустимых преобразований таблицы. Для этого находим ведущий элемент по формуле

θ_j = .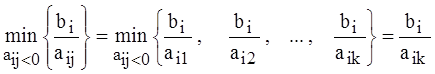

Пример 14.        Z(X) = x₁ + 2x₂ → max,

x₁ – x₂ + x₃ + 0x₄ + 0x₅ = -1 ,

x₁ – x₂ + 0x₃ - x₄ + 0x₅ = -3 ,

x₁ + 0x₂ + 0x₃ + 0x₄ + x₅ = 3 ,

x_i ≥ 0 ;    i = 1, 2, 3, 4, 5.

Решение. 1) Преобразуем расширенную матрицу

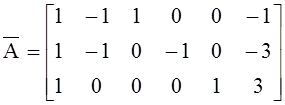 (-1)   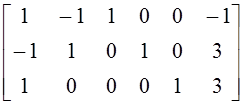 →   .Теперь матрица  имеет три базисных столбца А₃, А₄, А₅. В столбце В имеется отрицательное число b₁=-1.

№	Б	Сб	В	1	2	0	0	0
				A1	A2	A3	A4	A5
1	A3	0	-1	1	-1	1	0	0	(-1) (1)
2	A4	0	3	-1	1	0	1	0
3	A5	0	3	1	0	0	0	1
4			0	-1	-2	0	0	0

В строке 1 имеется отрицательный элемент а₁₂= -1, причем он стоит в столбце А₂. Можно найти ведущий элемент по формуле

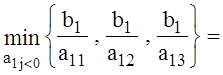
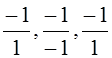      θ₂ =        =  =  ;  a₁₂ = -1.

При этом можно ввести в базис столбец А₂ с помощью допустимых преобразований таблицы.

3) Запишем симплексную таблицу.

В столбце В уже нет отрицательных чисел. Последняя строка показывает, что ∆_i ≤ 0, то есть допустимое решение Х₁ = (0, 1, 0, 2, 3) не оптимальное. Читателям рекомендуется завершить ее самостоятельно с помощью симплексных таблиц.  Ответ: max Z(X)=Z(X^*)=15 при Х^*=(3,6,2,0,0).

Пример 15. Z(X) = 5x₁ + 2x₂ → max,

x₁ + x₂ ≤ 3,

x₁ – x₂ ≤ -1,

x₁ + 3x₂ ≤ 1,

x_i ≥ 0, i = 1,2.

Решение. 1) Запишем задачу в основном виде: Z(X) = 5x₁ + 2x₂ → max,

x₁ + x₂ + x₃ + 0x₄ + 0x₅ = 3,

x₁ – x₂ +0 x₃ + x₄ + 0x₅ = -1,

x₁ + 3x₂ + 0x₃ + 0x₄ + x₅ = 1,

x_i ≥ 0, i = 1,2,3,4,5.

2) преобразуем расширенную матрицу.

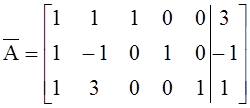     (-1) (1) (3)

3)Находим элемент преобразования матрицы по формуле

θ₂ = 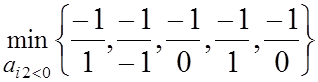 = ,а₂₂ = -1 элемент преобразования.

,

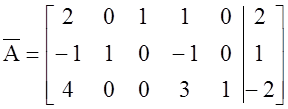 θ₃ =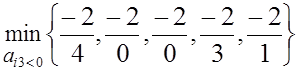 не существует, так как элементы левой части третей строки положительные, а элементы правой части–отрицательны, то в этом случае задача не имеет решения.

°3) Если столбцов с отрицательными а_ij в тех строках, где b_i < 0, несколько, то для сравнения можно подсчитать выгоду V_j = ∆_j∙ θ_j и выбрать столбец, где выгода V_j наибольшая.

Если V_j < 0 , так что наибольшая выгода может оказаться наименьшей по абсолютной величине и отрицательной, что приведет к увеличению значения Z(X).

Пример 16.      Z(X) = 3x₁ + 5x₂ – х₃ + 3х₄ – 6х₅ → min,

–x₁ – x₂ + 0x₃ – x₄ + 2x₅ + 0x₆ = -5 ,

0x₁ + x₂ + x₃ + x₄ + x₅ + 0x₆ = 3 ,

2x₁ + 0x₂ – x₃ – x₄ – 4x₅ – x₆ = 5 ,

x_i ≥ 0 ;    i = 1, 2, 3, 4, 5, 6.