Задача линейного программирования. Проверка оптимальности текущего плана, страница 16

8. В точке А = (2, 4) функция Z=x₁+x₂ принимает наименьшее значение  Z_min=Z (A) =2+4=6.                      

Согласно рис. 1 оптимальное решение единственное.

9. Перемещаем линию уровня Z=x₁+x₂ в направлении нормали .

Эта прямая в последний раз пересечет четырехугольник решений в точке С.

10. Определяем координаты С=(L₁)Ç(L₄). Решая систему

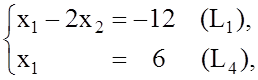 получаем.

11.В точке С = (6, 9) функция Z=x₁+x₂ принимает наибольшее значение, т.е. Z_max=Z(C) =6+9=15.

Согласно рис. 1 оптимальное решение  единственное.

Пример 2. Найти графически оптимальное решение системы неравенств

                                                                               (1)

                                                                              (2)

                                                                                (3)

                                                                                (4)

                                                                                     (5)

                                                                                          (6)                                             

минимизирующее максимизирующее и функцию Z=-4x₁+4x₂.

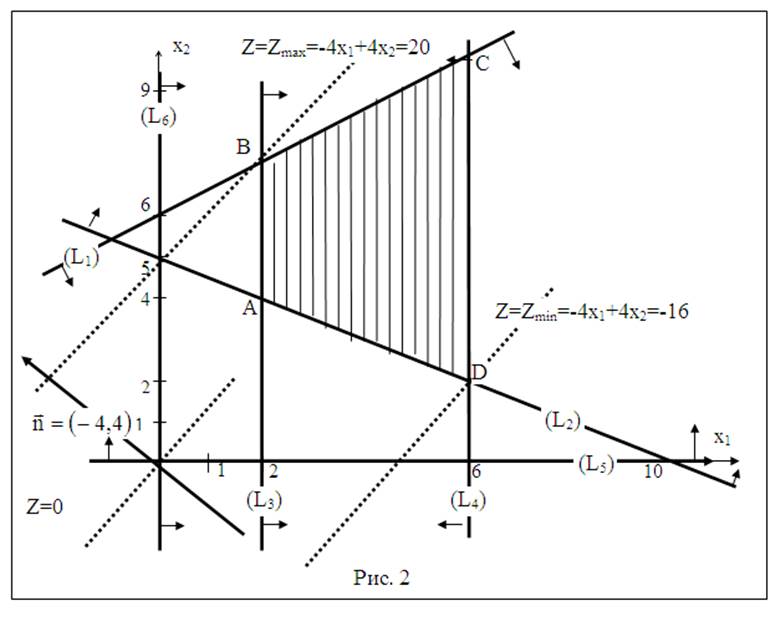
Решение.1. Строим область допустимых решений задачи подобно тому, как это сделано в примере 1. Областью решений данного примера является четырехугольник ABCD (см.рис. 2)

2. Строим нормаль линий уровня и одну из этих линий, например -4х₁ + 4х₂ = 0. Перемещаем линию уровня параллельно самой себе в направлении нормали .

В этом случае, как видно из рис. 2, первой общей точкой прямой Z с четырехугольником решений задачи является т. D и в ней Z(D)=Z_min.  Последней общей точкой является т. В и в ней Z(B)=Z_max.

3.йдем координаты т. В и т. D из решения системы уравнений:

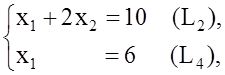   где т. D=(L₂)Ç(L₄), и

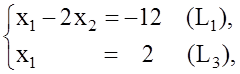где т. В=(L₁)Ç(L₃).

Отсюда D = (6, 2) и В = (2, 7), Z_min=Z(D)=-4∙6+4∙2=-16,  Z_max=Z (B) =-4∙2+4∙7=20.

Пример 3. Найти минимум максимум и функции Z=-3x₁+0∙x₂ при условиях:

                                                                                     (1)

                                                                               (2)

                                                                                       (3)

                                                                                             (4)

.                                                                                             (5)

Решение. 1. Строим область решений задачи. Для этого заменяем знаки неравенств в уравнениях ограничений на равенства:

                 (L₁),

            (L₂),

                     (L₃),

                          (L₄),     

                          (L₅).

Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение. Как видно из рис. 3, многоугольником решений задачи является треугольник АВС.

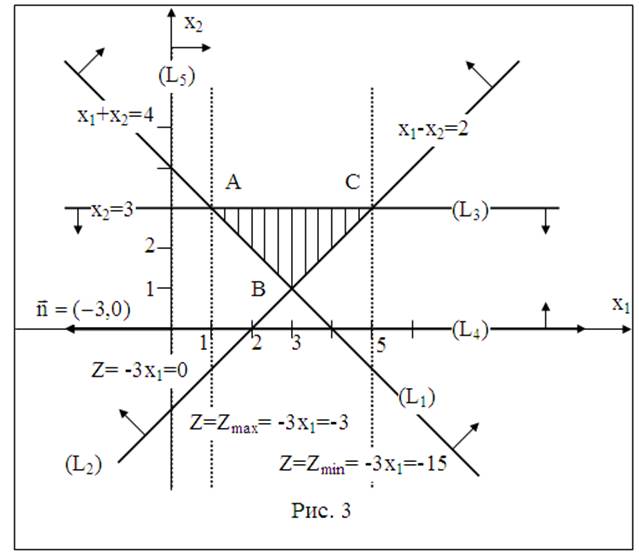
2. Строим нормаль линий уровня  прямой Z = 0. Передвигая данную прямую параллельно самой себе в направлении противоположном направлению линий уровня видим, что ее последней общей точкой с треугольником решений задачи является точка С. Следовательно в этой точке функция Z принимает минимальное значение, т.е. Z(C)=Z_min.

Первой общей точкой прямой Z с треугольником решений является т. А., Следовательно, в этой точке функция Z принимает максимальное значение, т.е. Z(А)=Z_max.

3.Нйдем координаты точек С и А решая систем уравнени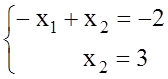й:

                и        .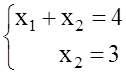

Отсюда С = (5, 3) и А= (1, 3), Z_min=Z(С)=-3∙5=-15, Z_max=Z(А)=-3∙1=-3.

Пример 4. Найти максимум и минимум функции Z=2x₁+2x₂ при условиях:

                                                                                     (1)

                                                                                             (2)

                                                                                             (3)

                                                                                             (4)