Задача линейного программирования. Проверка оптимальности текущего плана, страница 10

x_i ≥ 0, i = 1, 2, 3, 4, 5, 6.                                                                  (6)

3)Составим симплексную таблицу

Так как М – большое положительное число, то

∆₁ = 2М – 7  > 0, ∆₄ = 3М – 10  > 0. Произведем необходимые вычисления

θ₁ = min       = 2,     V₁ =  (2M – 7) ∙ (2) = 4M – 14 ;

θ₄ = min     = ,     V₄ =  (3M – 10) ∙  =;

Так как  V₄ >V₁ , то выгоднее включить в базис столбец А₄.

 При этом ведущим элементом будет  а₁₄ = 2.

4)Составим новую таблицу.

№	Б	Сб	В	7	-13	-8	10	М	М
				A1	A2	A3	A4	A5	A6
1	A4	10	3/2	1/2	-1/2	-3/2	1	1/2	0
2	A6	М	1/2	1/2	-3/2	1/2	0	-1/2	1	(2)(-1)
3			М+15	М-2	М+8	М-7	0	М+5	0

Произведем необходимые вычисления

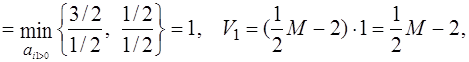θ ₁ θ₃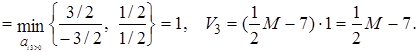

Так как  V₁ > V₃ , то ведущий элемент будет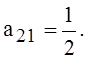  

5) Составим новую таблицу.                                        

№	Б	Сб	В	7	-13	-8	10	М	М
				A1	A2	A3	A4	A5	A6
1	A4	10	1	0	1	-2	1	1	-1	(1) (3)
2	A1	7	1	1	-3	-1	0	-1	2	+
3			17	0	2	-5	0	-М+3	-М+4

Итак, мы перешли к таблице, в которой А₅ и А₆ уже не являются базисными столбцами. Поэтому мы их зачеркнем. Произведем необходимые вычисления.

θ₂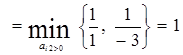 .Значит а₁₂ = 1 – ведущий элемент.

6) Составим новую таблицу.

Все оценки неположительные, значит текущий план Х^*= (4; 1; 0; 0) оптимален, ему соответствует минимальное значение функции  Z(Х) = 15.

Пример 11. Z(X) = - 3x₁ + x₂ → max,                                            (1)

 х₁ – 2х₂ + х₃ = 10 ,

-2х₁ – х₂ + 0х₃ = 10 ,                                                                         (2)