Задача линейного программирования. Проверка оптимальности текущего плана, страница 8

№	Б	Сб	В	5	0	0	0	0	0
				A1	A2	A3	A4	A5	A6
1	A1	5	2	1	0	-1	0	0	0
2	A4	0	2	0	0	1	1	0	0
3	A2	0	2	0	1	0	0	-1	0
4	A6	0	2	0	0	0	0	1	1	(1)
5			10	0	0	-5	0	0	0

2) Первоначальный план будет Х₀ = (2, 2, 0, 2, 0, 2).

3) Так как ∆_j ≤ 0 при j = 1,2,3,4,5,6,значит текущий план Х₀ оптимален и   minZ(X)=Z(X₀) =10.

4) Так как столбец А₅ небазисного столбца имеет нулевую оценку, значит данное оптимальное решение не единственное.

5) Этот столбец А₅ нужно ввести в базис, чтобы получить еще одно оптимальное решение. Для этого находим ведущий элемент преобразования по формуле:

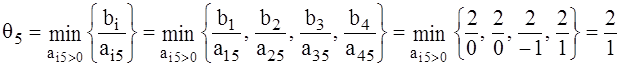,то есть а₄₅=1-ведущийэлемент.

6) Составим новую таблицу.

№	Б	Сб	В	5	0	0	0	0	0
				A1	A2	A3	A4	A5	A6
1	A1	5	2	1	0	-1	0	0	0
2	A4	0	2	0	0	1	1	0	0
3	A2	0	4	0	1	0	0	0	1
4	A5	0	2	0	0	0	0	1	1
5			10	0	0	-5	0	0	0

7) Второе оптимальное решение  Х₁^*= (2, 4, 0, 2, 2, 0).Вычисляем max Z(X) = 10.

8) Задача имеет бесконечное множество оптимальных решений Х^* = (1 – t) X₀^* + t X₁^*,   0 ≤ t ≤ 1  и  max Z(X) = 10.

Подставим в это уравнение найденные два оптимальные решения, получим формулу для определения любого оптимального решения задачи (общее решение)

Х^* = (1 – t) (2,2,0,2,0,2) + t (2,4,0,2,2,0) = (2 – 2t, 2 - 2t, 0, 2-2t, 0, 2 – 2t) +

+ (2t, 4t, 0, 2t, 2t, 0) = (2, 2 + 2t, 0, 2, 2t, 2 – 2t),     0 ≤ t ≤ 1.

Придавая параметру t любые числовые значения от 0 до 1, будем получать различные решения задачи, при любом из которых max Z (X) =10.

Например: при t = 0,X^* =(2,2,0,2,0,2)=X₀^*,t =1/2,X^*=(2,3,0,2,1,1),t=1,X^*=(2,4,0,2,2,0)=X₁^*.

1.2.7. Отсутствие конечного оптимума (min Z(X) = - ∞, max Z(X) = + ∞)

Теорема. 1^о) В задаче на минимум, если Δ_k > 0 для некоторого  j = k и среди чисел

a_ik (i=1, 2,…, m) нет положительных a_ik≤0 (т.е. в столбце А_к нет положительных элементов), то min Z(X) = - ∞.

2^о) В задаче на максимум, если Δ_k < 0 для некоторого   j = k и среди чисел a_ik (i=1, 2,…, m) нет положительных a_ij≤0 (т.е. в столбце А_к нет положительных элементов), то max Z(X) = ∞.

Пример 8.        Z (Х) = - х₁ - х₂ → min,

- x₁ + x₂ + x₃ = 1,

x₁ - 2x₂ + 1x₄ = 2,

x_i ≥ 0, i = 1, 2, 3, 4.

Решение. 1) Заполним первую симплекс - таблицу.

Первоначальное решение будет: Х₀ = (х₁ = 0, х₂ = 0, х₃ = 1, х₄ = 2) .